题目内容

20．已知双曲线$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}$=1的左右焦点分别为F1，F2，若双曲线左支上有一点M到右焦点F2距离为18，N为F2中点，O为坐标原点，则|NO|等于（　　）
A．$\frac{2}{3}$B．1C．2D．4

分析 利用ON是△MF1F2的中位线，ON=$\frac{1}{2}$MF1，再由双曲线的定义求出MF1，进而得到|ON|的值．

解答 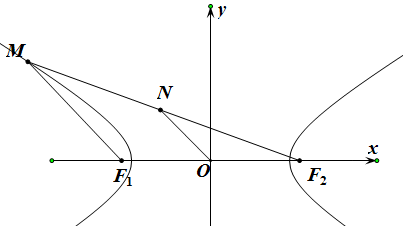解：∵双曲线$\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}$=1的左、右焦点分别为F1、F2，
左支上有一点M到右焦点F2的距离为18，N是MF2的中点，
连接MF1，ON是△MF1F2的中位线，∴ON∥MF1，ON=$\frac{1}{2}$MF1，
∵由双曲线的定义知，MF2-MF1=2×5，∴MF1=8．
∴ON=4，
故选D．

点评 本题以双曲线的标准方程为载体，考查双曲线的定义，考查三角形中位线的性质，属于基础题．

练习册系列答案
相关题目
19．某工厂要建造一个长方体无盖贮水池，其容积为6400m3，深为4m，如果池底每1m2的造价为300元，池壁每1m2的造价为240元，问怎样设计水池能使总造价最低，最低总造价是多少元？
11．已知奇函数f（x）的定义域为（-∞，0）∪（0，+∞），且不等式$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0对任意两个不相等的正实数x1，x2都成立，在下列不等式中，正确的是（　　）
A．f（-5）＞f（3）B．f（-5）＜f（3）C．f（-3）＞f（-5）D．f（-3）＜f（-5）
8．在（2x+a）5的展开式中，含x2项的系数等于320，则$\int_0^a{（{e^x}+2x）dx}$等于（　　）
A．e2+3B．e2+4C．e+1D．e+2
15．在△ABC中，角A，B，C所对边分别为a，b，c，若$B=30°，b=2，c=2\sqrt{3}$，则角C=60°或120°．
5．若数x，y满足$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{2x+y-7≤0}\end{array}}\right.$，则z=x-2y的最小值是（　　）
A．-3B．-4C．6D．-6
12．若$sin（{\frac{π}{3}-α}）=\frac{1}{3}$，则$cos（{\frac{π}{3}+2α}）$=（　　）
A．$\frac{7}{9}$B．$\frac{2}{3}$C．$-\frac{2}{3}$D．$-\frac{7}{9}$
9．化简：
（1）sin（$\frac{π}{6}$-2π）cos（$\frac{π}{4}$+π）
（2）sin（$\frac{π}{4}$+$\frac{5π}{2}$）
10．已知函数f（x）=lnx+ax．
（1）若曲线f（x）在点（1，f（1））处的切线与直线y=4x+1平行，求a的值；
（2）讨论函数f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网