题目内容
10．
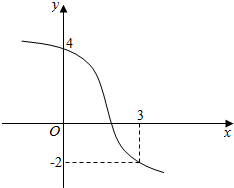已知函数f（x）的部分图象如图所示，若不等式-2＜f（x+t）＜4的解集为（-1，2），则实数t的值为-1．（写过程）
分析 根据图象的平移即可得到t的值．
解答 解：由图象可知，-2＜f（x）＜4的解集为（0，3），
不等式-2＜f（x+t）＜4的解集为（-1，2），
∴y=f（x+t）的图象是由y=f（x）的图象向右平移1个单位得到的，
∴t=-1，
故答案为：-1．
点评 本题考查了图象的平移和图象的识别，属于基础题．
练习册系列答案
相关题目
1．在复平面内，复数$\frac{2}{1-i}$+2i2对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
15．关于直线1和平面α，β，有如下三个命题：
①若直线l与平面α内的任意一条直线都没有公共点，则1∥α；
②若平面α内的任意一条直线与平面β都没有公共点，则α∥β；
③若直线1与平面α内的任意一条直线都垂直，则l⊥α．
在上述三个命题中，正确命题的个数为（ ）
①若直线l与平面α内的任意一条直线都没有公共点，则1∥α；
②若平面α内的任意一条直线与平面β都没有公共点，则α∥β；
③若直线1与平面α内的任意一条直线都垂直，则l⊥α．
在上述三个命题中，正确命题的个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
3．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点为F1，F2，P为椭圆上一点，且$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最小值是2c2，其中$c=\sqrt{{a^2}-{b^2}}$．则椭圆的离心率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |