题目内容
设S=
xe x2dx(其中e为自然对数的底),则S的值为 .
| ||
| 0 |
考点:定积分,二项式定理的应用
专题:导数的综合应用
分析:求出被积函数的原函数,然后分别代入积分上限和积分下限作差后得答案.
解答:
解:
xex2dx=
ex2
=
e4-
.
故答案为:
e4-
.
| ∫ | 2 0 |
| 1 |
| 2 |
| | | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了定积分,关键是求出被积函数的原函数,是基础题.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中,E、F分别是棱AB、BB1的中点,则A1E与CF所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

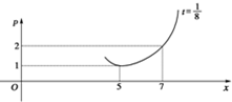 我国加入WTO时,根据达成的协议,若干年内某产品市场供应量p与关税的关系近似满足p(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,
我国加入WTO时,根据达成的协议,若干年内某产品市场供应量p与关税的关系近似满足p(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,




 下面四个命题:
下面四个命题: