题目内容
如图,四棱锥P—ABCD中,底面ABCD为平行四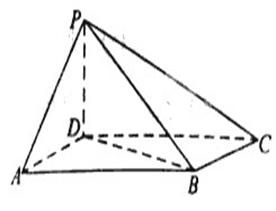 边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值。

(2)如图,以D为坐标原点,AD的长为单位长,DA、DB、DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系D-xyz,则
A(1,0,0),B(0, ,0),C(-1,
,0),C(-1, ,0),P(0,0,1),
,0),P(0,0,1),
 =(-1,
=(-1, ,0),
,0), =(0,
=(0, ,-1),
,-1), =(-1,0,0).
=(-1,0,0).

练习册系列答案
相关题目
 中,
中, ,则
,则 =( )
=( )  B.
B. C.
C. D.
D.
 的大致图象,则
的大致图象,则 等于
等于 B、
B、 C、
C、  D、
D、 


 到
到 ”左端需增加的代数式为( )
”左端需增加的代数式为( ) B.
B.  C.
C.  -
-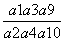 等于( )
等于( )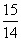 B.
B.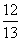 C.
C.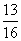 D.
D.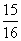

 (0<x<
(0<x< )
)
 -2
-2