Question

已知点O（0，0）、A（1，2）、B（4，5）及,

（1）t为何值时，P在x轴上？P在y轴上？P在第二象限？

（2）四边形OABP能否成为平行四边形？若能，求出相应的t值；若不能，请说明理由.

Answer 1

解:（1）∵=（1，2），=（4，5）-（1，2）=（3，3）,

∴=(1,2)+t(3,3)=(1+3t,2+3t).

当P在x轴上时，有2+3t=0,即t=-;

当P在y轴上时，有1+3t=0,即t=-;

当P在第二象限时，有

即-＜t＜-.

（2）∵=(1+3t,2+3t), =(3,3),

假如四边形OABP能成为平行四边形，则有=，即（1+3t，2+3t)=(3,3)，

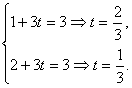∴该方程组无解，

∴假设不成立.

∴四边形不能成为平行四边形.