题目内容
设已知点O(0,0),A(1,2),B(4,5)及| OP |
| OA |
| AB |
分析:根据所给的三个点的坐标,写出
和
的坐标,利用向量的加减和数乘表示出
的坐标,横标和纵标都是含有t的代数式,根据所给的P的不同的位置,结合这个位置的坐标特点,写出t要满足的关系式,得到结果.
| OA |
| AB |
| OP |
解答:解:∵点O(0,0),A(1,2),B(4,5)及
=
+t
.
∴
=(1,2)+t(4-1,5-2)
=(1+3t,2+3t),
当P在x轴上时,它的坐标要满足纵标为0,
∴2+3t=0,
∴t=-
,
当P在y轴上,它的坐标要满足横标为0,
∴1+3t=0,
∴t=-
当P在第二象限时,1+3t<0,2+3t>0,
∴-
<t<-
| OP |
| OA |
| AB |
∴
| OP |
=(1+3t,2+3t),
当P在x轴上时,它的坐标要满足纵标为0,
∴2+3t=0,
∴t=-
| 2 |
| 3 |
当P在y轴上,它的坐标要满足横标为0,
∴1+3t=0,
∴t=-
| 1 |
| 3 |
当P在第二象限时,1+3t<0,2+3t>0,
∴-
| 2 |
| 3 |
| 1 |
| 3 |
点评:本题考查向量的坐标,考查向量的简单运算,是一个基础题,只要解题过程中比较细心,就可以得到本题的分数.

练习册系列答案
相关题目
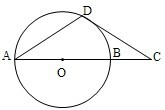 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. =
= +t
+t .求:t为何值时,P在x轴上?P在y轴上?P在第二象限?
.求:t为何值时,P在x轴上?P在y轴上?P在第二象限?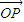 =
=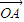 +t
+t .求:t为何值时,P在x轴上?P在y轴上?P在第二象限?
.求:t为何值时,P在x轴上?P在y轴上?P在第二象限?