题目内容
直线l：x=1与圆x2+y2-2y=0的位置关系是 ．
考点：直线与圆的位置关系
专题：直线与圆
分析：把圆的方程化为标准形式，根据圆心和半径可得它和直线l：x=1的关系．
解答：
解：圆x2+y2-2y=0，即 x2+（y-1）2 =1，表示以（0，1）为圆心、半径等于1的圆，
故此圆和直线l：x=1相切，
故答案为：相切．
故此圆和直线l：x=1相切，
故答案为：相切．
点评：本题主要考查直线和圆的位置关系判定，圆的标准方程，属于基础题．
练习册系列答案
相关题目
已知抛物线C1：x2=4py，圆C2：x2+（y-p）2=p2，直线l：y=| 1 |
| 2 |
| AB |
| CD |
A、
| ||
B、
| ||
C、
| ||
| D、p2 |
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
| D、若命题p：“?x0∈R使x02+x0+1＜0”，则￢p为假命题 |
直线y=kx+3与圆（x-2）2+（y-3）2=4相交于M、N两点，若|MN|≤2
，则k的取值范围是（ ）
| 3 |
A、[
| ||||||||
B、(0，
| ||||||||
C、(-∞，-
| ||||||||
D、[-
|
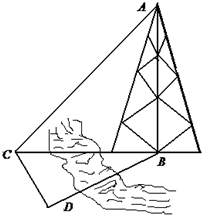如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C，D．现测得∠BCD=60°，∠DBC=45°，CD=20m，并在点C测得塔顶A的仰角为45°，求塔高AB（精确到0.1，