题目内容
5.已知(x2-$\frac{1}{x}$)${\;}^{{n}^{\;}}$展开式的所有项的二项式系数和为32,则展开式中x4项的系数为10.分析 由题意可得:2n=32,解得n.再利用二项式定理的通项公式即可得出.
解答 解:由题意可得:2n=32,解得n=5.
∴Tr+1=${∁}_{5}^{r}$(x2)5-r$(-\frac{1}{x})^{r}$=(-1)r${∁}_{5}^{r}$x10-3r,
令10-3r=4,解得r=2.
∴展开式中x4项的系数为$(-1)^{2}{∁}_{5}^{2}$=10.
故答案为:10.
点评 本题考查了二项式定理的应用、考查了推理能力与计算能力,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
16.已知命题P:?x∈[1,2],x2-2x-1>0,则P的否定是( )
| A. | ¬P:?x∈(-∞,1)∪(2,+∞),x2-2x-1>0 | B. | ¬P:?x∈[1,2],x2-2x-1>0 | ||
| C. | ¬P:?x∈(-∞,1)∪(2,+∞),x2-2x-1≤0 | D. | ¬P:?x∈[1,2],x2-2x-1≤0 |
17.据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3000人进行调查,就“是否取消英语听力”的问题进行了问卷调查统计,结果如表:
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数X的分布列和数学期望.
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数X的分布列和数学期望.
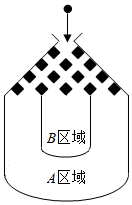 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$. 对于实数a和b,定义运算a*b,运算原理如图所示,若(1+m)*(1-m)=2,则实数m=0,或1,或-1.
对于实数a和b,定义运算a*b,运算原理如图所示,若(1+m)*(1-m)=2,则实数m=0,或1,或-1.