题目内容
13.已知函数f(x)=x2+bx+c(b,c∈R)满足f(b)≥f(c),记f(x)的最小值为m(b,c).(Ⅰ)证明:当b>0时,m(b,c)≤1;
(Ⅱ)当b,c满足m(b,c)≥1时,求f(1)的最大值.
分析 (Ⅰ)根据不等式的性质结合一元二次函数的性质即可证明:当b>0时,m(b,c)≤1;
(Ⅱ)根据不等式的进行转化求解即可.
解答 解:(Ⅰ)由f(b)≥f(c)得:2b2≥c2+bc
即(c+2b)(c-b)≤0
又 b>0∴-2b≤c≤b,
$m(b,c)=c-\frac{1}{4}{b^2}≤b-\frac{1}{4}{b^2}≤1$(当且仅当b=c=2时等号成立)…(6分)
(Ⅱ)由$m(b,c)=c-\frac{1}{4}{b^2}≥1$得:$c≥\frac{1}{4}{b^2}+1$
又(c+2b)(c-b)≤0
ⅰ)当b>0时,-2b≤c≤b,∴$b≥c≥\frac{1}{4}{b^2}+1$
即b2-4b+4≤0
解得b=2
代入$b≥c≥\frac{1}{4}{b^2}+1$得c=2
所以f(1)=5
ⅱ)当b<0时,b≤c≤-2b,∴$-2b≥c≥\frac{1}{4}{b^2}+1$
即b2+8b+4≤0
解得$-4-2\sqrt{3}≤b≤-4+2\sqrt{3}$,
$f(1)=1+b+c≤1+b-2b=1-b≤5+2\sqrt{3}$
当$b=-4-2\sqrt{3},c=8+4\sqrt{3}$时等号成立.
ⅲ)当b=0时,c=0,与题意不符.
综上知:f(1)的最大值为$5+2\sqrt{3}$. …(14分)
点评 本题主要考查函数最值的求解以及不等式的应用,利用不等式的性质进行转化推理是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
8.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与圆(x-2)2+y2=3相切,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
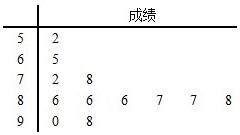 为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.
为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.