题目内容
5.函数f(x)=($\frac{1}{3}$)x+x-5的零点为x1、x2,函数g(x)=log${\;}_{\frac{1}{3}}$x+x-5的零点为x3、x4,则x1+x2+x3+x4的值为10.分析 由函数与方程的关系转化为图象的交点问题,根据同底的指数函数和对数函数互为反函数,图象关于y=x对称的性质进行转化求解.
解答 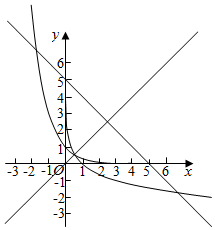 解:由f(x)=($\frac{1}{3}$)x+x-5=0得($\frac{1}{3}$)x=5-x,
解:由f(x)=($\frac{1}{3}$)x+x-5=0得($\frac{1}{3}$)x=5-x,
由g(x)=log${\;}_{\frac{1}{3}}$x+x-5的得log${\;}_{\frac{1}{3}}$x=5-x
分别作出函数y=($\frac{1}{3}$)x,y=5-x和y=log${\;}_{\frac{1}{3}}$x的图象,
∵y=($\frac{1}{3}$)x和y=log${\;}_{\frac{1}{3}}$x的图象关于y=x对称,
则($\frac{1}{3}$)x=5-x,与log${\;}_{\frac{1}{3}}$x=5-x的根关于y=x对称,
由$\left\{\begin{array}{l}{y=x}\\{y=5-x}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{5}{2}}\end{array}\right.$,
即两直线的交点坐标为($\frac{5}{2}$,$\frac{5}{2}$),
则$\frac{{x}_{1}+{x}_{3}}{2}$=$\frac{5}{2}$,$\frac{{x}_{2}+{x}_{4}}{2}$=$\frac{5}{2}$,
即x1+x3=5,x2+x4=5,
则x1+x2+x3+x4=10,
故答案为:10.
点评 本题主要考查函数与零点的应用,结合指数函数和对数函数的对称性是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
20.已知双曲线x2-my2=1的离心率为3,则其渐近线与圆(x-3)2+y2=7的位置关系为( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 无法判断 |
17.为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:
附:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
则有( )的把握认为环保知识是否优秀与性别有关.
| 优秀 | 非优秀 | 总计 | |
| 男生 | 40 | 20 | 60 |
| 女生 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.500 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |