题目内容
已知(1+x)n=1+a1x+a2x2+…+anxn,n∈N*且Sn=a1+2a2+…+nan,n∈N*,n=3时,S3= ;当n∈N*时,
Si= .
| n |
 |
| i=1 |
考点:二项式系数的性质
专题:二项式定理
分析:当n=3时,利用二项式定理求得a1、a2、a3的值,可得S3=a1+2a2+3an的值,化简
Si=
+(
+2
)+(
+2
+3
)+…+(
+2
+3
+…+n
).对于等式(1+x)n=1+a1x+a2x2+…+anxn,令x=1并且两边同时取导数可得n2n-1=a1+2a2+3a3+…+nan,可得
Si=1×1+2×21+3×22+…+n•2n-1,再用错位相减法求得
Si 的值.
| n |
 |
| i=1 |
| C | 1 n |
| C | 1 n |
| C | 2 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
解答:
解:当n=3时,∵(1+x)3=1+3x+3x2+3x3,∴a1=3,a2=3,a3=1,
∴S3=a1+2a2+3an=3+6+3=12.
Si=a1+(a1+2a2)+(a1+2a2+3a3)+…+(a1+2a2+3a3+…+nan)
=
+(
+2
)+(
+2
+3
)+…+(
+2
+3
+…+n
).
对于等式(1+x)n=1+a1x+a2x2+…+anxn,令x=1并且两边同时取导数可得,n2n-1=a1+2a2+3a3+…+nan,
∴
Si=1×1+2×21+3×22+…+n•2n-1,
∴2
Si=1×2+2×22+3×23+…+n•2n,
错位相减法可得-
Si=1+2+22+23+…+2n-1-n2n =
-n2n=(1-n)2n-1,
花简求得
Si=(n-1)×2n +1,
故答案为:12;(n-1)×2n +1.
∴S3=a1+2a2+3an=3+6+3=12.
| n |
 |
| i=1 |
=
| C | 1 n |
| C | 1 n |
| C | 2 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
对于等式(1+x)n=1+a1x+a2x2+…+anxn,令x=1并且两边同时取导数可得,n2n-1=a1+2a2+3a3+…+nan,
∴
| n |
 |
| i=1 |
∴2
| n |
 |
| i=1 |
错位相减法可得-
| n |
 |
| i=1 |
| 1×(1-2n) |
| 1-2 |
花简求得
| n |
 |
| i=1 |
故答案为:12;(n-1)×2n +1.
点评:本题主要考查二项式定理的应用,求展开式中某项的系数,二项式系数的性质,用错位相减法进行数列求和,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若实数a,b,c满足a2+b2+c2=8,则a+b+c的最大值为( )
| A、9 | ||
B、2
| ||
C、3
| ||
D、2
|
给出下列四个命题,其中假命题是( )
| A、从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样 | ||
| B、样本方差反映了样本数据与样本平均值的偏离程度 | ||
| C、在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 | ||
D、设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(-1<x<0)=
|
 如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则这三个数位于不同行不同列的概率是
如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则这三个数位于不同行不同列的概率是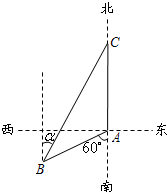 如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?
如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?