题目内容
(本小题满分12分)已知平面上的动点 及两定点
及两定点 、
、 ,直线
,直线 、
、 的斜率分别为
的斜率分别为 、
、 ,且
,且 ,设动点
,设动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)过点 的直线与曲线
的直线与曲线 交于两点M、N,过点
交于两点M、N,过点 作
作
 轴,交曲线
轴,交曲线 于点
于点 .求证:直线
.求证:直线 过定点,并求出定点坐标.
过定点,并求出定点坐标.
(1)由题知 ,且
,且 ,
, ,则
,则 .
.
整理得曲线 的方程为
的方程为
 5分
5分
(2)设直线 与
与 轴交于
轴交于 ,
,
则直线 的方程为
的方程为 ,记
,记 ,
, ,由对称性知
,由对称性知 ,
,
由 ,消去
,消去 得
得 , 7分
, 7分
所以 ,且
,且 ,
, , 9分
, 9分
由 三点共线知,
三点共线知, ,即
,即 ,所以
,所以 ,
,
整理得 , 10分
, 10分
所以, ,即
,即 ,解得
,解得 ,
,
所以直线 过定点
过定点 12分
12分
【解析】
试题分析(1)由题知x≠±2,且 ,
, ,由直接法求出曲线C的方程.
,由直接法求出曲线C的方程.
(2)设NQ与x轴交于D(t,0),则直线NQ的方程为x=my+t(m≠0),记N(x1,y1),Q(x2,y2),由对称性知M(x2,﹣y2),由 ,得(3m2+4)y2+6mty+3t2﹣12=0,由此利用根的判别式,韦达定理、三点共线,结合已知条件能证明直线NQ过定点D(1,0).
,得(3m2+4)y2+6mty+3t2﹣12=0,由此利用根的判别式,韦达定理、三点共线,结合已知条件能证明直线NQ过定点D(1,0).
考点:直线与圆锥曲线的综合问题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
已知实数x,y满足条件
则-
的取值范围是( )
|
| x+1 |
| y+2 |
A、[-
| ||||
B、[-5,-
| ||||
C、[
| ||||
D、[
|
 设
设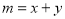 ,若
,若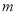 的最大值为6,则
的最大值为6,则 的最小值为( )
的最小值为( ) )如下图所示,此几何体的体积是_____________
)如下图所示,此几何体的体积是_____________

 ,
, ) B.(
) B.( ) C.(
) C.( 、
、 ,
, 且
且 ,若
,若 ,则
,则
 ,
,
 ,若
,若 ,则
,则 的最小值为
的最小值为 B.
B. C.
C. D.
D.
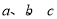 成等比数列的充要条件是
成等比数列的充要条件是
 的等比数列是递减数列
的等比数列是递减数列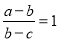 是
是 成等差数列的充分不必要条件
成等差数列的充分不必要条件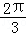 ,则线段AB的长度为( )
,则线段AB的长度为( ) C.2 D.2
C.2 D.2