题目内容
已知函数y=|cosx+sinx|.
(1)画出函数在x∈[-
,
]上的简图;
(2)写出函数的最小正周期和在[-
,
]上的单调递增区间;试问:当x在R上取何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.
(1)画出函数在x∈[-
| π |
| 4 |
| 7π |
| 4 |
(2)写出函数的最小正周期和在[-
| π |
| 4 |
| 3π |
| 4 |
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.
考点:五点法作函数y=Asin(ωx+φ)的图象,三角形的形状判断
专题:三角函数的图像与性质
分析:(1)将函数进行化简即可画出函数在x∈[-
,
]上的简图;
(2)根据函数图象即可写出函数的最小正周期和在[-
,
]上的单调递增区间,并求出最值.
(3)求出x的大小即可判断△ABC的形状.
| π |
| 4 |
| 7π |
| 4 |
(2)根据函数图象即可写出函数的最小正周期和在[-
| π |
| 4 |
| 3π |
| 4 |
(3)求出x的大小即可判断△ABC的形状.
解答:
解:(1)∵y=|cosx+sinx|=
|sin(x+
)|,
∴当x∈[-
,
]时,其图象如图所示.
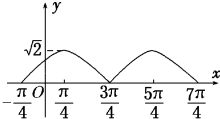
(2)函数的最小正周期是π,在[-
,
]上的单调递增区间是[-
,
];由图象可以看出,
当x=kπ+
(k∈Z)时,该函数有最大值,最大值是
.
(3)若x是△ABC的一个内角,则有0<x<π,
∴0<2x<2π.
由y2=1得|cosx+sinx|2=1.
即1+sin2x=1,即sin2x=0,
则2x=π,解得x=
,
即△ABC为直角三角形.
| 2 |
| π |
| 4 |
∴当x∈[-
| π |
| 4 |
| 7π |
| 4 |

(2)函数的最小正周期是π,在[-
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
当x=kπ+
| π |
| 4 |
| 2 |
(3)若x是△ABC的一个内角,则有0<x<π,
∴0<2x<2π.
由y2=1得|cosx+sinx|2=1.
即1+sin2x=1,即sin2x=0,
则2x=π,解得x=
| π |
| 2 |
即△ABC为直角三角形.
点评:本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的图象,单调性,最值性质的求解和应用.

练习册系列答案
相关题目
数列{3n2-28n}中,各项中最小的项是( )
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
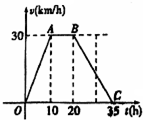 据气象中心观察和预测:发生于沿海M地的台风一直想正南方向移动,其运动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂下l,梯形OABC在直线l左侧部分的面积即为t(h)内台风所经过的路程s(km)
据气象中心观察和预测:发生于沿海M地的台风一直想正南方向移动,其运动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂下l,梯形OABC在直线l左侧部分的面积即为t(h)内台风所经过的路程s(km)