题目内容
已知函数f(x)=Asin(ωx+φ),其中ω>0.
(1)当A=ω=2,φ=
时,函数g(x)=f(x)-m在[0,
]上有两个零点,求m的范围;
(2)当A=1,φ=
时,若函数f(x)图象的相邻两条对称轴之间的距离等于
,求函数f(x)的解析式,并求最小正实数n,使得函数f(x)的图象向左平移n个单位所对应的函数是奇函数.
(1)当A=ω=2,φ=
| π |
| 6 |
| π |
| 2 |
(2)当A=1,φ=
| π |
| 6 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由题意可得函数y=f(x)的图象和直线y=m在[0,
]上有两个交点,数形结合求得m的范围.
(2)由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得y=sin(2x+2n+
)为奇函数,可得2n+
=kπ,k∈z,由此求得n的最小值.
| π |
| 2 |
(2)由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得y=sin(2x+2n+
| π |
| 6 |
| π |
| 6 |
解答:
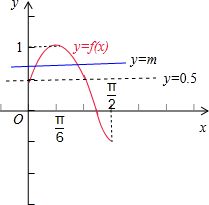 解:(1)当A=ω=2,φ=
解:(1)当A=ω=2,φ=
时,f(x)=2sin(2x+
),
则由题意可得函数y=f(x)的图象和直线y=m在[0,
]上有两个交点,
如图所示:
故m的范围为[1,2).
(2)当A=1,φ=
时,若函数f(x)=sin(ωx+
),图象的相邻两条对称轴之间的距离等于
,
可得
=2×
,ω=2,故f(x)=sin(2x+
).
把函数f(x)的图象向左平移n个单位所对应的函数的解析式为
y=sin[2(x+n)+
]=sin(2x+2n+
),
再根据y=sin(2x+2n+
)为奇函数,
可得2n+
=kπ,k∈z,
故n的最小值为
.
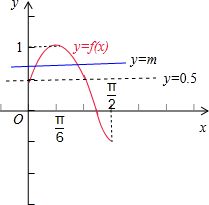 解:(1)当A=ω=2,φ=
解:(1)当A=ω=2,φ=| π |
| 6 |
| π |
| 6 |
则由题意可得函数y=f(x)的图象和直线y=m在[0,
| π |
| 2 |
如图所示:
故m的范围为[1,2).
(2)当A=1,φ=
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
可得
| 2π |
| ω |
| π |
| 2 |
| π |
| 6 |
把函数f(x)的图象向左平移n个单位所对应的函数的解析式为
y=sin[2(x+n)+
| π |
| 6 |
| π |
| 6 |
再根据y=sin(2x+2n+
| π |
| 6 |
可得2n+
| π |
| 6 |
故n的最小值为
| 5π |
| 12 |
点评:本题主要考查方程根的存在性以及个数判断,正弦函数的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,体现了数形结合、转化的数学思想,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
如图,阴影部分的面积是( )
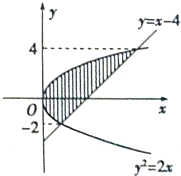

| A、16 | B、18 | C、20 | D、22 |
已知函数f(x)=
,若对任意xx≠x2,都有
<0成立,则a的取值范围是( )
|
| f(x1)-f(x ) |
| x1-x2 |
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(-1,2) |
若a、b、c为实数,且a>b,则下面一定成立的是( )
| A、ac>bc |
| B、a2>b2 |
| C、a+c>b |
| D、a-c>b-c |