题目内容
ξ~B(7.0.5),P(ξ=k)最大时,k= .
考点:二项分布与n次独立重复试验的模型
专题:计算题
分析:根据ξ~B(7.0.5),可得P(ξ=k)=
×(
)7-2k,利用
是先增后减,(
)7-2k是减函数,可得P(ξ=k)=
×(
)7-2k是先增后减,从而计算概率的值,即可得到结论.
| C | k 7 |
| 1 |
| 2 |
| C | k 7 |
| 1 |
| 2 |
| C | k 7 |
| 1 |
| 2 |
解答:
解:∵ξ~B(7.0.5),
∴P(ξ=k)=
×(
)7-2k
∵
是先增后减,(
)7-2k是减函数
∴P(ξ=k)=
×(
)7-2k是先增后减
∵P(ξ=3)=
×(
) =
,P(ξ=4)=
×(
)-1=70,P(ξ=5)=
×(
)-3=168,P(ξ=6)=
×(
)-5=224
P(ξ=7)=
×(
)-7=128
∴k=6时,P(ξ=k)最大
故答案为:6
∴P(ξ=k)=
| C | k 7 |
| 1 |
| 2 |
∵
| C | k 7 |
| 1 |
| 2 |
∴P(ξ=k)=
| C | k 7 |
| 1 |
| 2 |
∵P(ξ=3)=
| C | 3 7 |
| 1 |
| 2 |
| 35 |
| 2 |
| C | 4 7 |
| 1 |
| 2 |
| C | 5 7 |
| 1 |
| 2 |
| C | 6 7 |
| 1 |
| 2 |
P(ξ=7)=
| C | 7 7 |
| 1 |
| 2 |
∴k=6时,P(ξ=k)最大
故答案为:6
点评:本题以二项分布为载体,考查概率的最大值,解题的关键是利用随机变量的分布列,进行计算,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
设函数f(x)=
sin2ωx+cos2ωx,其中0<ω<2.
(1)若f(x)的周期为π,求f(x)的单调增区间;
(2)若函数f(x)的图象的一条对称轴为x=
,求f(x)在x∈[0,π]的值域.
| ||
| 2 |
(1)若f(x)的周期为π,求f(x)的单调增区间;
(2)若函数f(x)的图象的一条对称轴为x=
| π |
| 3 |
下表是X的分布列,则a=( )
| X | 1 | 2 | 3 |
| P | 0.5 | a | 0.3 |
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
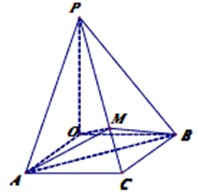 如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=