题目内容
已知an+1=nan+n-1,a1=1,求数列{an}的通项公式.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由an+1=nan+n-1得1+an+1=n(an+1),利用累积法进行求解即可.
解答:
解:∵an+1=nan+n-1,
∴1+an+1=n(an+1),即
=n,
则
=1,
=2,
=3,…
=n-1,
等式两边同时相乘得
•
•
…,
=1×2×3×…(n-1),
即
=(n-1)!,
则1+an=2•(n-1)!,
即an=2•(n-1)!-1.
故数列{an}的通项公式an=2•(n-1)!.
∴1+an+1=n(an+1),即
| 1+an+1 |
| 1+an |
则
| 1+a2 |
| 1+a1 |
| 1+a3 |
| 1+a2 |
| 1+a4 |
| 1+a3 |
| 1+an |
| 1+an-1 |
等式两边同时相乘得
| 1+a2 |
| 1+a1 |
| 1+a3 |
| 1+a2 |
| 1+a4 |
| 1+a3 |
| 1+an |
| 1+an-1 |
即
| 1+an |
| 2 |
则1+an=2•(n-1)!,
即an=2•(n-1)!-1.
故数列{an}的通项公式an=2•(n-1)!.
点评:本题主要考查数列通项公式的求解,根据数列的递推关系,利用累积法是解决本题的关键.

练习册系列答案
相关题目
已知长方体ABCD-A1B1C1D1,AB=
,BC=1,AA1=2,则该长方体的外接球体积为( )
| 3 |
| A、8π | ||||
B、
| ||||
C、
| ||||
D、12
|
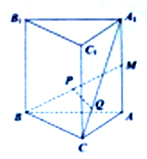 在直三棱柱ABC-A1B1C1中,若BC⊥AC,∠A=
在直三棱柱ABC-A1B1C1中,若BC⊥AC,∠A=