题目内容
sin315°-cos495°+2sin210°的值是（ ）
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式中的角度变形后，利用诱导公式化简，再利用特殊角的三角函数值计算即可得到结果．
解答：
解：原式=sin（360°-45°）-cos（540°-45°）+2sin（180°+30°）
=-sin45°+cos45°-2sin30°
=-
+
-2×
=-1．
故选：B．
=-sin45°+cos45°-2sin30°
=-
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=-1．
故选：B．
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
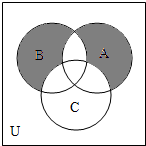如图所示，已知集合A、B、C为全集U的子集，则图中阴影部分所表示的集合为（ ）| A、（∁∪C）∪（A∪B） |
| B、（A∪B）∩[∁∪（A∩B）] |
| C、（A∪B）∩[∁∪（A∩B∩C）] |
| D、{A∩[∁∪（B∪C）]}∪{B∩[∁∪（A∪C）]} |
已知变量x，y满足条件：
，则z=
的取值范围（ ）
|
| y |
| x |
| A、[1，2] | ||||
B、[1，
| ||||
C、[-1，
| ||||
D、[
|
在如图所示的茎叶图中，中位数和众数分别是（ ）
| A、93，92 |
| B、92，93 |
| C、91，93 |
| D、93，93 |
设复数z=
（i为虚数单位）的共轭复数是（ ）
| 2+i |
| 2i-1 |
| A、-i | ||
| B、i | ||
C、
| ||
D、-
|
若两个集合A、B是非空集合，则“A∩B=B”是“A∪B=A”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知x，y满足约束条件
，那么z=2x+3y的最小值为（ ）
|
A、
| ||
| B、8 | ||
C、
| ||
| D、10 |