题目内容
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3…
(1)证明数列{lg(1+an)}是等比数列
(2)设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项
(3)记bn=
+
,设数列{bn}的前n项和Sn,证明
≤Sn<1.
(1)证明数列{lg(1+an)}是等比数列
(2)设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项
(3)记bn=
| 1 |
| an |
| 1 |
| an+2 |
| 3 |
| 4 |
考点:数列与不等式的综合,等比关系的确定
专题:等差数列与等比数列
分析:(1)把点(an,an+1)代入函数式,整理得an+1+1=(an+1)2,两边取对数整理得
=2,进而判断{lg(1+an)}是公比为2的等比数列,;
(2)根据等比数列的通项公式求的数列{lg(1+an)}的通项公式,进而求的an代入到Tn=(1+a1)(1+a2)(1+an)求的Tn;
(3)将an+1=an2+2an因式分解后取倒数,再裂项得到
=
-
,代入bn化简后再利用相消法求出Sn,再根据n的取值和式子的特点求出其范围.
| lg(1+an+1) |
| lg(1+an) |
(2)根据等比数列的通项公式求的数列{lg(1+an)}的通项公式,进而求的an代入到Tn=(1+a1)(1+a2)(1+an)求的Tn;
(3)将an+1=an2+2an因式分解后取倒数,再裂项得到
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
解答:
解:(1)由已知an+1=an2+2an,∴an+1+1=(an+1)2
∵a1=2
∴a1+1=3>1,两边取对数得lg(1+an+1)=2lg(1+an),
即
=2,
∴{lg(1+an)}是lg3为首项,公比为2的等比数列.
(2)由(1)知lg(1+an)=2n-1•lg3=lg32n-1,
∴1+an=32n-1,则an=32n-1-1
∴Tn=(1+a1)(1+a2)(1+an)=320•321•322…32n-1
=31+2+22+…+2n-1=32n-1,
(3)∵an+1=an2+2an,∴an+1=an(an+2),
∴
=
=
(
-
),
则
=
-
,
∴bn=
+
=
-
,
∴Sn=b1+b2+…+bn=2[(
-
)+(
-
)+…+(
-
)]
=2(
-
),
∵an=32n-1-1,a1=2,an+1=32n-1
∴Sn=1-
<1,且随着n的增大而增大,
∵n=1,2,3…,
∴当n=1时,Sn有最小值是1-
=
故
≤Sn<1.
∵a1=2
∴a1+1=3>1,两边取对数得lg(1+an+1)=2lg(1+an),
即
| lg(1+an+1) |
| lg(1+an) |
∴{lg(1+an)}是lg3为首项,公比为2的等比数列.
(2)由(1)知lg(1+an)=2n-1•lg3=lg32n-1,
∴1+an=32n-1,则an=32n-1-1
∴Tn=(1+a1)(1+a2)(1+an)=320•321•322…32n-1
=31+2+22+…+2n-1=32n-1,
(3)∵an+1=an2+2an,∴an+1=an(an+2),
∴
| 1 |
| an+1 |
| 1 |
| an(an+2) |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an+2 |
则
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
∴bn=
| 1 |
| an |
| 1 |
| an+2 |
| 2 |
| an |
| 2 |
| an+1 |
∴Sn=b1+b2+…+bn=2[(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
=2(
| 1 |
| a1 |
| 1 |
| an+1 |
∵an=32n-1-1,a1=2,an+1=32n-1
∴Sn=1-
| 2 |
| 32n-1 |
∵n=1,2,3…,
∴当n=1时,Sn有最小值是1-
| 2 |
| 32-1 |
| 3 |
| 4 |
故
| 3 |
| 4 |
点评:本题主要考查了等比关系的确定和数列的求和问题,考查了学生对数列知识的综合掌握,灵活化简、变形能力.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
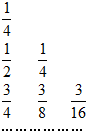 下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).
下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).