Question

9．点P到椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$上的任意一点，F₁，F₂是它的两个焦点，O为坐标原点，$\overrightarrow{OQ}=\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}$，则动点Q的轨迹方程是$\frac{x^2}{16}+\frac{y^2}{12}=1$．

Answer 1

分析 由向量的共线定义，则$\overrightarrow{OP}$=-$\overrightarrow{OQ}$=（-$\frac{x}{2}$，-$\frac{y}{2}$），代入椭圆方程，即可求得动点Q的轨迹方程．

解答 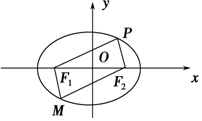解：设Q（x，y），由$\overrightarrow{OQ}=\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}$，则$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$=$\overrightarrow{PM}$=2$\overrightarrow{PO}$=-2$\overrightarrow{OP}$，
∴$\overrightarrow{OP}$=-$\frac{1}{2}$$\overrightarrow{OQ}$=（-$\frac{x}{2}$，-$\frac{y}{2}$），
∵P是椭圆上$\frac{x^2}{4}+\frac{y^2}{3}=1$的任意一点，则P（-$\frac{x}{2}$，-$\frac{y}{2}$），
代入椭圆方程：$\frac{（-\frac{x}{2}）^{2}}{4}+\frac{（-\frac{y}{2}）^{2}}{3}=1$，整理得：$\frac{x^2}{16}+\frac{y^2}{12}=1$．
故答案：$\frac{x^2}{16}+\frac{y^2}{12}=1$．

点评 本题考查动点的轨迹方程的求法，解题时要认真审题，注意向量运算法则的合理运用，属于中档题，．