题目内容
18.已知函数f(x)满足f(x+1)=-x2-4x+l,函数g(x)=$\left\{\begin{array}{l}{f(x)-4,x≤m}\\{x-4,x>m}\end{array}\right.$有两个零点,则m的取值范围为[-2,0)∪[4,+∞).分析 利用函数的关系式求出函数的解析式,求出函数的最值,画出函数的图象,通过m与1比较,讨论函数的解得个数,求解即可.
解答 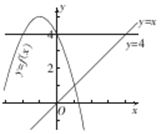 解:函数f(x)满足f(x+1)=-x2-4x+l,可得函数f(x)=-x2-2x+4,函数的最大值为:f(-1)=5,当f(x)=x时,x=1或-4,故函数y=f(x)与直线y=x的两个交点分别为(1,1)(-4,-4),当f(x)=4时,x=0或-2,由题意可知m≠1,当m<1时,直线y=4与y=x(x>m)有一个公共点,故直线y=4与y=f(x)(x≤m)有且只有一个公共点,故-2≤m<0.
解:函数f(x)满足f(x+1)=-x2-4x+l,可得函数f(x)=-x2-2x+4,函数的最大值为:f(-1)=5,当f(x)=x时,x=1或-4,故函数y=f(x)与直线y=x的两个交点分别为(1,1)(-4,-4),当f(x)=4时,x=0或-2,由题意可知m≠1,当m<1时,直线y=4与y=x(x>m)有一个公共点,故直线y=4与y=f(x)(x≤m)有且只有一个公共点,故-2≤m<0.
当m>1时,直线y=4与y=f(x)(x≤m)有2个公共点,故直线y=4与y=x(x>m)无公共点,故m≥4.综上,m的取值范围是:[-2,0)∪[4,+∞).
故答案为:[-2,0)∪[4,+∞).
点评 本题考查函数的零点判定定理的应用考查数形结合以及分类讨论思想的应用.

练习册系列答案
相关题目
8.某大学的男生的体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立回归方程$\stackrel{∧}{y}$=0.85x-85.71,则下列结论中不正确的是( )
| A. | y与x具有正的线性相关关系 | |
| B. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg | |
| C. | 过该大学某女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 回归直线过样本的中心$(\overline x,\overline y)$ |
 如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上
如图,ABC-A1B1C1是底面边长为2,高为$\frac{\sqrt{3}}{2}$的正三棱柱,经过AB的截面与上