题目内容
若不等式|mx3-lnx|≥1(m>0),对?x∈(0,1]恒成立,则实数m的取值范围是 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:根据绝对值不等式的性质,结合不等式恒成立,利用参数分离法,构造函数,求函数的导数以及函数的最值即可.
解答:
解:|mx3-lnx|≥1对任意x∈(0,1]都成立
等价为mx3-lnx≥1,或mx3-lnx≤-1,
即m≥
,记为f(x),或m≤
,记为g(x),
f'(x)=
=
,
由f'(x)=
=0,
解得lnx=-
,即x=e-
,
由f(x)>0,解得0<x<e-
,此时函数单调递增,
由f(x)<0,解得x>e-
,此时函数单调递减,
即当x=e-
时,函数f(x)取得极大值,同时也是最大值f(e-
)=
=
=
e2,此时m≥
e2,
若m≤
,
∵当x=1时,
=0,
∴当m>0时,不等式m≤
不恒成立,
综上m≥
e2.
故答案为:m≥
e2.
等价为mx3-lnx≥1,或mx3-lnx≤-1,
即m≥
| 1+lnx |
| x3 |
| lnx-1 |
| x3 |
f'(x)=
| ||
| x6 |
| -2-3lnx |
| x4 |
由f'(x)=
| -2-3lnx |
| x4 |
解得lnx=-
| 2 |
| 3 |
| 2 |
| 3 |
由f(x)>0,解得0<x<e-
| 2 |
| 3 |
由f(x)<0,解得x>e-
| 2 |
| 3 |
即当x=e-
| 2 |
| 3 |
| 2 |
| 3 |
1+lne-
| ||
(e-
|
1-
| ||
| e-2 |
| 1 |
| 3 |
| 1 |
| 3 |
若m≤
| lnx-1 |
| x3 |
∵当x=1时,
| lnx-1 |
| x3 |
∴当m>0时,不等式m≤
| lnx-1 |
| x3 |
综上m≥
| 1 |
| 3 |
故答案为:m≥
| 1 |
| 3 |
点评:本题主要考查不等式恒成立问题,构造函数,利用函数的导数和最值之间的关系,利用参数分离法是解决本题的关键.综合性较强,运算量较大.

练习册系列答案
相关题目
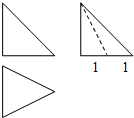 一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为
一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为