题目内容
9．sin410°cos145°+sin680°sin（-35°）=$\frac{\sqrt{2}-\sqrt{6}}{4}$．分析 由条件利用诱导公式、两角和差的三角公式，求得要求式子的值．
解答 解：sin410°cos145°+sin680°sin（-35°）=sin50°（-cos35°）+sin（-40°）sin（-35°）
=-sin50°cos35°+sin40°sin35°=-sin50°cos35°+cos50°sin35°
=sin（35°-50°）=-sin15°=-sin（45°-30°）=-（sin45°cos30°-cos45°sin30°）
-（$\frac{\sqrt{2}}{2}•\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}•\frac{1}{2}$）=$\frac{\sqrt{2}-\sqrt{6}}{4}$，
故答案为：$\frac{\sqrt{2}-\sqrt{6}}{4}$．
点评 本题主要考查诱导公式、两角和差的三角公式的应用，属于基础题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
1．
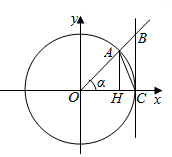如图所示，在单位圆O中，∠AOH=α（0＜α＜$\frac{π}{2}$），若△AOH的面积记为S1，△BOC的面积记为S2，△AOC的面积为S3，扇形AOC的面积记为S4，则（ ）
如图所示，在单位圆O中，∠AOH=α（0＜α＜$\frac{π}{2}$），若△AOH的面积记为S1，△BOC的面积记为S2，△AOC的面积为S3，扇形AOC的面积记为S4，则（ ）| A． | S1=$\frac{1}{2}$sinα | B． | S2=$\frac{1}{2}$tanα | C． | S3=α | D． | S4=$\frac{1}{2}$cosα |
18．已知函数f（x）=2sin（ωx+$\frac{π}{3}$）（ω＞0）在区间（0，π）上存在唯一一个x0∈（0，π），使得f（x0）=1，则ω的取值范围为（ ）
| A． | （$\frac{1}{2}$，$\frac{11}{6}$] | B． | [$\frac{1}{2}$，$\frac{11}{6}$） | C． | （$\frac{1}{3}$，$\frac{13}{6}$] | D． | [$\frac{1}{3}$，$\frac{13}{6}$） |