题目内容
10.已知抛物线x2=8y的焦点F到双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线的距离为$\frac{4\sqrt{5}}{5}$,点P是抛物线x2=8y上一动点,P到双曲线C的右焦点F2的距离与到直线y=-2的距离之和的最小值为3,则该双曲线的标准方程为$\frac{x^2}{4}$-y2=1.分析 确定抛物线的焦点坐标,双曲线的渐近线方程,进而可得a=2b,再利用抛物线的定义,结合P到双曲线C的右焦点F2(c,0)的距离与到直线y=-2的距离之和的最小值为3,可得FF2=3,从而可求双曲线的几何量,从而可得结论.
解答 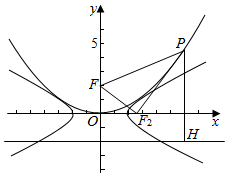 解:抛物线x2=8y的焦点F(0,2),
解:抛物线x2=8y的焦点F(0,2),
双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)一条渐近线的方程为bx-ay=0,
由抛物线x2=8y的焦点F到双曲线C的渐近线的距离为$\frac{4\sqrt{5}}{5}$,
可得d=$\frac{2a}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{4\sqrt{5}}{5}$,
即有2b=a,
由P到双曲线C的右焦点F2(c,0)的距离与到直线y=-2的距离之和的最小值为3,
由抛物线的定义可得P到准线的距离即为P到焦点F的距离,
可得|PF2|+|PF|的最小值为3,
连接FF2,可得|FF2|=3,
即c2+4=9,
解得c=$\sqrt{5}$,
由c2=a2+b2,a=2b,
解得a=2,b=1,
则双曲线的方程为$\frac{x^2}{4}$-y2=1.
故答案为:$\frac{x^2}{4}$-y2=1.
点评 本题主要考查了抛物线、双曲线的几何性质,考查抛物线的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
10.已知集合A={1,2,3},B={3,4},则A∪B=( )
| A. | {1,2} | B. | {1,2,3,4} | C. | {1,2,3} | D. | {1,2,4} |
7.设a=($\frac{3}{4}$)0.5,b=($\frac{4}{3}$)0.4,c=log${\;}_{\frac{3}{4}}$(log34),则a,b,c相互之间的大小关系为c<a<b.
19.将函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后的图象关于y轴对称,则函数f(x)在[0,$\frac{π}{2}$]上的最小值为( )
| A. | 0 | B. | -1 | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
20.已知{an}为等比数列,a1=3,且4a1,2a2,a3成等差数列,则a3+a5等于( )
| A. | 189 | B. | 72 | C. | 60 | D. | 33 |