题目内容
4.若2sin2x+cos2x=1(x≠kπ,k∈Z),则$\frac{2co{s}^{2}x+sin2x}{1+tanx}$的值为$\frac{2}{5}$.分析 由二倍角公式和已知式子可得tanx=2,弦化切并整体代入计算可得.
解答 解:∵2sin2x+cos2x=1,∴4sinxcosx=1-cos2x=2sin2x,
解得sinx=0或2cosx-sinx=0,∵x≠kπ,k∈Z,
∴sinx=0不成立,故2cosx-sinx=0,即tanx=2,
∴$\frac{2co{s}^{2}x+sin2x}{1+tanx}$=$\frac{1}{3}$(2cos2x+sin2x)
=$\frac{1}{3}$•$\frac{2co{s}^{2}x+2sinxcosx}{co{s}^{2}x+si{n}^{2}x}$=$\frac{1}{3}$•$\frac{2+2tanx}{1+ta{n}^{2}x}$=$\frac{2}{5}$,
故答案为:$\frac{2}{5}$.
点评 本题考查同角三角函数基本关系,涉及二倍角公式以及弦化切的思想,属中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
14.若集合A={1,m2},B={2,9},则“m=3”是“A∩B={9}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中百位数字比十位数字大,十位数字比个位数字大的有( )个.
| A. | 100 | B. | 120 | C. | 300 | D. | 600 |
8.已知命题p:?x0∈R,x0-2>0,命题q:?x∈R,2x>x2,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
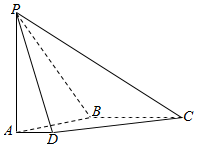 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AD∥BC,侧棱PA⊥底面ABCD,且PA=AB=BC=2,AD=1.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AD∥BC,侧棱PA⊥底面ABCD,且PA=AB=BC=2,AD=1.