题目内容
15.在(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式中,含x3项的系数是64(用数字填写答案)分析 根据二项式展开式的通项公式,令展开式中含x项的指数等于3,求出r的值,即可求出展开式中x3项的系数.
解答 解:二项式(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6展开式的通项公式为
Tr+1=${C}_{6}^{r}$•${(2\sqrt{x})}^{6-r}$•${(-\frac{1}{\sqrt{x}})}^{r}$=(-1)r•26-r•${C}_{6}^{r}$•x3-r,
令3-r=3,
解得r=0;
∴展开式中x3项的系数是26×${C}_{6}^{0}$=64.
故答案为:64.
点评 本题考查了利用二项式展开式的通项公式求展开式中特定项的系数问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知命题p:?x∈R,log3x≥0,则( )
| A. | ¬p:?x∈R,log3x≤0 | B. | ¬p:?x∈R,log3x≤0 | C. | ¬p:?x∈R,log3x<0 | D. | ¬p:?x∈R,log3x<0 |
6.已知函数f(x)的对应关系如表:
若函数f(x)不存在反函数,则实数m的取值集合为{-2,1,3,5}.
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | 3 | -2 | 1 | 5 | m |
3.方程9x+|3x+b|=5(b∈R)有两个负实数解,则b的取值范囤为( )
| A. | (3,5) | B. | (-5.25,-5) | C. | [-5.25,-5) | D. | 前三个都不正确 |
10.若tanα=-$\sqrt{3}$且α是第四象限角,则sinα的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | ±$\frac{\sqrt{3}}{2}$ |
20.设k是一个正整数,$(1+\frac{x}{k}{)^4}$的展开式中x3的系数为$\frac{1}{16}$,记函数y=x2与y=kx的图象所围成的阴影部分为S,任取x∈[0,4],y∈[0,16],则点(x,y)恰好落在阴影区域S内的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{5}$ |
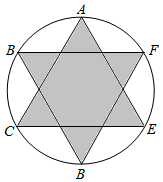 如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.
如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.