为了丰富学生的课余生活.增加学生的阅读面.亳州一中南校计划在综合楼建造一个室内面积为800平方米的矩形电子阅览室.在阅览室内沿左右两侧与后墙内侧各保留1m宽的通道.沿前侧内墙保留3m的空地.当矩形阅览室边长各为多少时.面积最大.最大为多少? 题目和参考答案——青夏教育精英家教网—

题目内容

为了丰富学生的课余生活，增加学生的阅读面，亳州一中南校计划在综合楼建造一个室内面积为800平方米的矩形电子阅览室，在阅览室内沿左右两侧与后墙内侧各保留1m宽的通道，沿前侧内墙保留3m的空地，当矩形阅览室边长各为多少时，面积最大，最大为多少？

考点：函数模型的选择与应用

专题：函数的性质及应用,不等式的解法及应用

分析：设出矩形的长为a与宽b，建立蔬菜面积关于矩形边长的函数关系式S=（a-4）（b-2）=ab-4b-2a+8=808-2（a+2b）．利用基本不等式变形求解．

解答： 解：设阅览室的左侧边长为a m，后侧边长为b m，则 ab=800，
面积S=（a-4）（b-2）=ab-4b-2a+8=808-2（a+2b），
因为a+2b≥2

2ab

，
所以S≤808-4

2ab

=648，
当且仅当a=2b，即a=40（m），b=20（m），
S取最大值648，
答：当阅览室的左侧边长为40m，后侧边长为20m时，面积最大，为648m2．

点评：此类问题一般用函数最值来求解，本题别出心裁，利用基本不等式求解，设计巧妙．

练习册系列答案

相关题目

若f（x）是R上周期为5的奇函数，且满足f（1）=1，f（2）=3，则f（8）+f（4）的值为

．

命题p：“?x₀∈R，x₀²+2x₀+2≤0”，则命题p的否定?p是

．

已知等差数列{a_n}满足：a₅=5，a₂+a₆=8．
（1）求{a_n}的通项公式；
（2）若b_n=a_n+2^a_n，求数列{b_n}的前n项和S_n．

所确定的平面区域为D．
（1）记平面区域D的面积为S=f（t），试求f（t）的表达式．
（2）设向量

=（1，-1），

=（2，-1），Q（x，y）在平面区域D（含边界）上，

，（m，n∈R），当面积S取到最大值时，用x，y表示m+3n，并求m+3n的最大值．

已知函数f（x）=

bx+c

x+1

的图象过原点，且关于点（-1，1）成中心对称．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若数列{a_n}（n∈N^*）满足：a_n＞0，a₁=1，a_n+1=（f（

））²，求数列{a_n}的通项a_n；
（Ⅲ）若数列{a_n}的前项和为S_n，判断S_n，与2的大小关系，并证明你的结论．

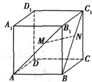如图，在正方体ABCD-A₁B₁C₁D₁中，M、N分别是对角线AB₁、BC₁上的点，且

B1M

C1N

，求证：MN∥平面A₁B₁C₁D₁（写出三种作法）

设曲线y=

x-1

x+1

在点（-2，f（2））处的切线与直线ax+y+1=0垂直，则实数a=（　　）

试题分类