题目内容
10.已知全集U=R,集合A={x|-5<x<7},B={x|a+1<x<2a+15}.(1)若a=0,求A∪B和∁UB;
(2)若A∩B=B,求实数a的取值范围.
分析 (1)若a=0,B={x|1<x<15},进而可得求A∪B和∁UB;
(2)若A∩B=B,则B⊆A,进而可得实数a的取值范围.
解答 (本题满分14分)
解:(1)当a=0时,B={x|1<x<15},又A={x|-5<x<7},
所以A∪B={x|-5<x<15},∁UB={x|x≤1,或x≥15},.…(7分)
(2)由A∩B=B可知B⊆A.
当a+1≥2a+15即a≤-14时,B=∅,满足题意;
当a+1<2a+15即a>-14时,B≠∅,由B⊆A可得,$\left\{\begin{array}{l}a>-14\\ a+1≥-5\\ 2a+15≤7\end{array}\right.$解得-6≤a≤-4.
综上可得,实数a的取值范围a≤-14或-6≤a≤-4.…(14分)
点评 本题考查的知识点是集合的包含关系判断及应用,集合的交集,并集,补集运算,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在一个口袋中装5个白球和3个黑球,这些球除颜色外完全相同,从中摸出1个球,则摸到黑球的概率是( )
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
20.若函数f(x)是定义在R上的奇函数,但当x>0时,f(x)=$\frac{1}{x+1}$-log2(x+1),则满足4f(x+1)>7的实数x的取值范围是( )
| A. | (2,+∞) | B. | (-∞,-1)∪(3,+∞) | C. | (-4,2) | D. | (-∞,-4) |
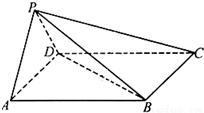 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD.