Question

4．若2kπ+π＜θ＜2kπ+$\frac{5π}{4}$（k∈Z），则sinθ，cosθ，tanθ的大小关系是cosθ＜sinθ＜tanθ．

Answer 1

分析 根据角θ的范围画出三角函数线，再由三角函数线判断正弦，余弦，正切的大小关系．

解答 解：当2kπ+π＜θ＜2kπ+$\frac{5π}{4}$（k∈Z），
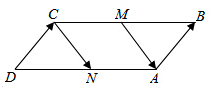
其终边在第三象限，如右图，
正弦线：MP（负），
余弦线：OM（负），
正切线：AT（正），
因为角θ的终边在第三象限平分线的上方，
所以，|OM|＞|MP|，
再考察符号，cosθ＜sinθ＜0＜tanθ，
故答案为：cosθ＜sinθ＜tanθ．

点评 本题主要考查了三角函数线的应用，涉及三角函数符号的判断和数值大小的比较，属于基础题．