题目内容
19．如图，在四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$，N、M分是AD、BC上的点，且$\overrightarrow{CN}$=$\overrightarrow{MA}$，求证：$\overrightarrow{DN}$=$\overrightarrow{MB}$．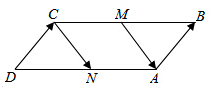
分析 利用向量相等与向量的加法即可得出．
解答 证明：∵$\overrightarrow{AB}$=$\overrightarrow{DC}$，N、M分是AD、BC上的点，且$\overrightarrow{CN}$=$\overrightarrow{MA}$，
∴$\overrightarrow{DC}$+$\overrightarrow{CN}$=$\overrightarrow{MA}$+$\overrightarrow{AB}$
∵$\overrightarrow{DN}$=$\overrightarrow{DC}$+$\overrightarrow{CN}$，$\overrightarrow{MB}$=$\overrightarrow{MA}$+$\overrightarrow{AB}$
∴$\overrightarrow{DN}$=$\overrightarrow{MB}$．
点评 本题考查了向量相等与向量的加法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
9．《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过3500元的部分不必纳税，超过3500元的部分为全月应纳税所得额．此项税款按下表分段累计计算：
（1）设某人月工资、薪金所得为x元，求应纳税款Y的函数表达式？
（2）某人一月份应交纳此项税款为303元，那么他当月的工资，薪金所得是多少？
| 全月应纳税所得额 | 税率（%） |
| 不超过1500元的部分 | 3 |
| 超过1500元至4500元的部分 | 10 |
| 超过4500元至9000元的部分 | 20 |
（2）某人一月份应交纳此项税款为303元，那么他当月的工资，薪金所得是多少？
10．已知X～N（μ，σ2）时，P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974，则$\int_3^4{\frac{1}{{\sqrt{2π}}}}{e^{-\frac{{{{（{x-1}）}^2}}}{2}}}$dx=（ ）
| A． | 0.043 | B． | 0.0215 | C． | 0.3413 | D． | 0.4772 |
7．下列四个函数中，在（0，+∞）上是增函数的是（ ）
| A． | f（x）=3-x | B． | f（x）=x2-3x | C． | f（x）=x-1 | D． | $f（x）={x^{\frac{1}{2}}}$ |
某小区设计一屋顶阁楼的截面图为等腰三角形，顶角为120°，腰长为4m，预备要开一矩形窗户，窗宽为x（m），试求：