题目内容
13.已知函数f(x)=|x2+3x|,x∈R,若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为(0,1)∪(9,+∞).分析 由y=f(x)-a|x-1|=0得f(x)=a|x-1|,作出函数y=f(x),y=a|x-1|的图象,利用数形结合即可得到结论.
解答 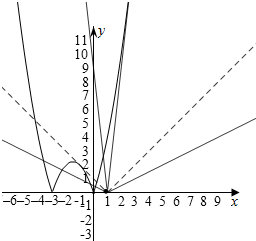 解:由y=f(x)-a|x-1|=0得f(x)=a|x-1|,
解:由y=f(x)-a|x-1|=0得f(x)=a|x-1|,
作出函数y=f(x),y=g(x)=a|x-1|的图象,
当a≤0,f(x)≥0,g(x)≤0,两个函数的图象
不可能有4个交点,不满足条件;
则a>0,此时g(x)=a|x-1|=$\left\{\begin{array}{l}{a(x-1),x≥1}\\{-a(x-1),x<1}\end{array}\right.$,
当-3<x<0时,f(x)=-x2-3x,g(x)=-a(x-1),
当直线和抛物线相切时,有三个零点,
此时-x2-3x=-a(x-1),
即x2+(3-a)x+a=0,
则由△=(3-a)2-4a=0,即a2-10a+9=0,
解得a=1或a=9,
当a=9时,g(x)=-9(x-1),g(0)=9,此时不成立,∴此时a=1,
要使两个函数有四个零点,则此时0<a<1,
若a>1,此时g(x)=-a(x-1)与f(x),有两个交点,
此时只需要当x>1时,f(x)=g(x)有两个不同的零点即可,
即x2+3x=a(x-1),整理得x2+(3-a)x+a=0,
则由△=(3-a)2-4a>0,即a2-10a+9>0,解得a<1(舍去)或a>9,
综上a的取值范围是(0,1)∪(9,+∞).
故答案为:(0,1)∪(9,+∞).
点评 本题主要考查函数零点个数的应用,利用数形结合是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
18.定义在R上的函数f(x)的图象是连续不断的,且自变量与对应的函数值有如下关系:
那么函数f(x)一定存在零点的区间是(2,3).
| x | … | 1 | 2 | 3 | … |
| f(x) | … | 3 | 4 | -1 | … |