题目内容

在渤海中有一座小岛，小岛上矗立着一座山，为了测量山的高度，在海平面上选择了相距800米的A、B两点，在A点测得山顶C的仰角为45°，∠BAD=120°，又在B点测得∠ABD=45°，其中点D是点C到水平面的垂足，求山高CD．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：求出DE，可得AD，因为在A点测得山顶C的仰角为45°，D是点C到水平面的垂足，所以山高CD=AD，即可得出结论．
解答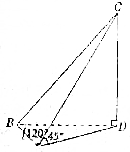： 解：在三角形ABD中，∠BAD=120°，∠ABD=45°，所以∠ADB=15°．
过D做DE垂直BA延长线与E，则DE=BE，∠ADE=30°，
所以AE=
1
2
AD=BE-AB=DE-AB=
1
3
DE，
解得DE=1200+400
3
，所以AD=800+800
3
．
因为在A点测得山顶C的仰角为45°，D是点C到水平面的垂足，
所以山高CD=AD=800+800
3
（m）．
点评：本题考查利用数学知识解决实际问题，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
设函数f（x）=（
1
2
）|x|，x∈R
（1）请画出函数f（x）的大致图象；
（2）若不等式f（x）+f（2x）≤k对于任意的x∈R恒成立，求实数k的取值范围．
2014年国庆节期间，甲、乙、丙、丁四位同学决定去A、B两个学校参观学习，私人约定通过抛硬币的形式决定自己是去A校还是B校，每人抛掷2枚硬币一次，若都是正面向上则去A校，其余情况则去B校，假设每人抛掷硬币是相互独立的．
（Ⅰ）求这四人中去A校的人数大于去B校的人数的概率；
（Ⅱ）记去A校的人数为X，求X的分布列和均值（数学期望）．
已知直角三角形ABC的斜边长AB=2，现以斜边AB为轴旋转一周，得旋转体，当∠A=30°时，求此旋转体的体积与表面积的大小．
数列{an}满足a1=1，an=2an-1-3n+6（n≥2，n∈N+）．
（1）设bn=an-3n，求证：数列{bn}是等比数列；
（2）求数列{an}的通项公式．
下表是某校1～5月份的用电量（单位：百度）的一组数据：
月份x12345
用电量y4.5432.53
用电量y与月份x之间有较好的线性相关关系，其线性回归方程为
?
y
=-0.7x+a，则a=
 
．
某出版社出版的一本书，若以每本15元的价格发行，可发行40000本．当每本书的定价每提高1元时，发行量就减少2000本．
（1）写出销售收入y（元）与定价x（元）之间的函数关系式；
（2）要使收入不低于500000元，则这本书的最高定价为多少元？
在△ABC中，内角A，B，C的对边分别为a，b，c，且b2+c2+bc-a2=0，则=
asin(30°-C)
b-c
（　　）
A、-
1
2
B、
1
2
C、-
3
2
D、
3
2
在等比数列{an}中，a2=2，a4=8，则a6=（　　）
A、64B、32C、28D、14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网