题目内容
设函数f(x)=(
)|x|,x∈R
(1)请画出函数f(x)的大致图象;
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,求实数k的取值范围.
| 1 |
| 2 |
(1)请画出函数f(x)的大致图象;
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,求实数k的取值范围.
考点:函数的图象,函数恒成立问题
专题:函数的性质及应用
分析:(1)化为分段函数,可作出图象;或者先做出x≥0时的函数图象,再根据f(x)是偶函数,图象关于y轴对称,作出x<0的图象.
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,只要(f(x)+f(2x))min≤k对于任意的x∈R恒成立即可,将f(x)的解析式代入,利用换元法转化为二次函数求最值即可.
(2)若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,只要(f(x)+f(2x))min≤k对于任意的x∈R恒成立即可,将f(x)的解析式代入,利用换元法转化为二次函数求最值即可.
解答:
解(1)∵f(x)=(
)|x|
则函数的图象如图所示;

(2)∵f(x)=(
)|x|,
∴f(2x)=(
)|2x|,
∵不等式f(x)+f(2x)≤k对于任意的x∈R恒成立
令t=(
)|x|=t∈(0,1],则y=t2+t(0<t≤1)
∵对称轴t=-
,则当t=1时,ymax=2,
∴k≥2
| 1 |
| 2 |
|
则函数的图象如图所示;

(2)∵f(x)=(
| 1 |
| 2 |
∴f(2x)=(
| 1 |
| 2 |
∵不等式f(x)+f(2x)≤k对于任意的x∈R恒成立
令t=(
| 1 |
| 2 |
∵对称轴t=-
| 1 |
| 2 |
∴k≥2
点评:本题考查含有绝对值的函数的图象的做法和不等式恒成立为题,题目难度不大,属基本题型,基本方法的考查.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
将函数y=cosx的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移
个单位,所得函数图象的一条对称轴方程是( )
| π |
| 4 |
| A、x=π | ||
B、x=
| ||
C、x=
| ||
D、x=
|
阅读程序框图,若m、n分别是双曲线
-
=1的虚轴长和实半轴长,则输出a,i别是( ) 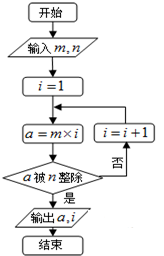
| x2 |
| 36 |
| y2 |
| 4 |

| A、a=12,i=3 |
| B、a=12,i=4 |
| C、a=8,i=3 |
| D、a=8,i=4 |
已知命题p:“?x∈[1,2],x2-a≥0”,命题q:“?x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
| A、{a|a≥1} |
| B、{a|a≤-2或1≤a≤2} |
| C、{a|-2≤a≤1} |
| D、{a|a≤-2或a=1} |
设m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列为假命题的是( )
| A、若m⊥α,n∥α,则m⊥n |
| B、若α∥β,β∥γ,m⊥α,则m⊥γ |
| C、若m⊥α,n⊥β,m∥n,则α∥β |
| D、若α⊥γ,β⊥γ,则α∥β |
