题目内容
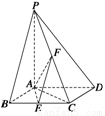
如图所示,已知四棱锥的底面是菱形,侧面PDA和侧面PDC所成的二面角为120°,且都垂直于底面,另两个侧面与底面所成的角都等于60°.
(1)求异面直线PB与AC所成的角;
(2)求直线PC与底面ABCD所成的角.
解:如图,作DE⊥BC,垂足为E,连结PE、AC,

∵平面PAD⊥平面AC,平面PDC⊥平面AC,平面PDA∩平面PDC=PD,
∴PD⊥平面AC,∠PED是二面角PBCD的平面角,∠PED=60°,
∠ADC是二面角APDC的平面角,∠ADC=120°.
(1)由于AC⊥BD,
∴AC⊥PB,而AC、PB所成角是90°.
(2)∠PCD即为PC与底面ABCD所成角,设PD=h,则在Rt△PDE中,DE=PD·cot60°=![]() ,
,
∵四边形ABCD是菱形,∴∠DCE=60°.
于是,DC=![]() ,
,
∴tan∠PCD=![]() .
.
∴PC与底面ABCD所成角为arctan![]() .
.

练习册系列答案
相关题目
 如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足
如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且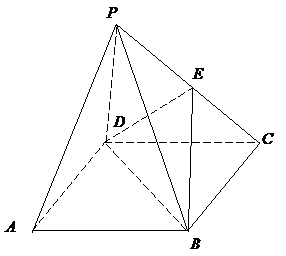
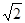 .
.
 ,
,