题目内容
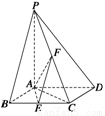
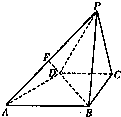 如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足
如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足| PF |
| PA |
(1)证明:PA⊥BD;
(2)当λ取何值时,直线DF与平面ABCD所成角为30°?
分析:(1)先证明PO⊥平面ABCD,再建立空间直角坐标系,利用向量的数量积为0,可证得PA⊥BD;
(2)利用平面ABCD的一个法向量
=(0,0,1),直线DF与平面ABCD所成角为30°,根据向量的夹角公式,即可求得结论.
(2)利用平面ABCD的一个法向量
| n |
解答: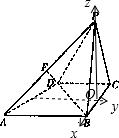 (1)证明:如图,∵△PBC是等边三角形,O是BC中点,∴PO⊥BC.
(1)证明:如图,∵△PBC是等边三角形,O是BC中点,∴PO⊥BC.
由侧面PBC⊥底面ABCD,得PO⊥平面ABCD,
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O-xyz.
∵AB=BC=PB=PC=2CD=2,
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,
)
∴
=(-2,-1,0),
=(1,-2,-
)
∴
•
=-2+2+0=0
∴
⊥
∴PA⊥BD;
(2)解:∵
=λ
,
=(1,-2,-
)
∴
=(λ,-2λ,-
λ)
∵
=(1,1,
)
∴
=
+
=(1+λ,1-2λ,
-
λ)
∵平面ABCD的一个法向量
=(0,0,1),直线DF与平面ABCD所成角为30°
∴sin30°=|
|
∴4λ2-16λ+7=0
∴λ1=
,λ2=
(舍去)
∴λ=
时,直线DF与平面ABCD所成角为30°.
 (1)证明:如图,∵△PBC是等边三角形,O是BC中点,∴PO⊥BC.
(1)证明:如图,∵△PBC是等边三角形,O是BC中点,∴PO⊥BC.由侧面PBC⊥底面ABCD,得PO⊥平面ABCD,
以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O-xyz.
∵AB=BC=PB=PC=2CD=2,
∴A(1,-2,0),B(1,0,0),D(-1,-1,0),P(0,0,
| 3 |
∴
| BD |
| PA |
| 3 |
∴
| BD |
| PA |
∴
| BD |
| PA |
∴PA⊥BD;
(2)解:∵
| PF |
| PA |
| PA |
| 3 |
∴
| PF |
| 3 |
∵
| DP |
| 3 |
∴
| DF |
| DP |
| PF |
| 3 |
| 3 |
∵平面ABCD的一个法向量
| n |
∴sin30°=|
| ||||
|
|
∴4λ2-16λ+7=0
∴λ1=
| 1 |
| 2 |
| 7 |
| 2 |
∴λ=
| 1 |
| 2 |
点评:本题考查线线垂直,考查线面角,考查李建勇空间向量解决立体几何问题,属于中档题.

练习册系列答案
相关题目
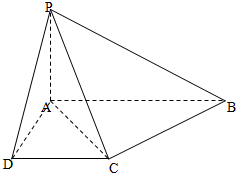 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且
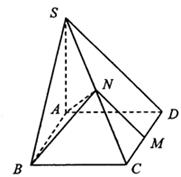
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且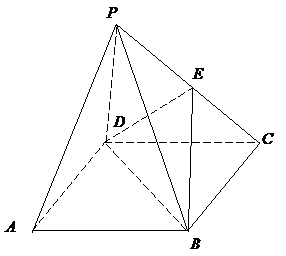
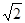 .
.
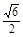 ,
,