题目内容
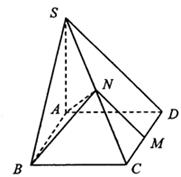
(本题满分12分)如图所示,已知四棱锥S—ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB=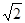 .
.
(1)求证:MN⊥平面ABN;(2)求二面角A—BN—C的余弦值
【答案】
(1)见解析; (2)所求的二面角的余弦值为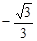 。
。
【解析】
试题分析:(Ⅰ)建立空间直角坐标系,求出向量 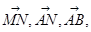 ,计算
,计算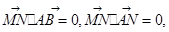 从而证明∴
从而证明∴ 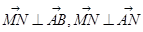 即可证明MN⊥平面ABN;
即可证明MN⊥平面ABN;
(II)求平面NBC的法向量,平面ABN的法向量,利用向量的数量积求得二面角A-BN-C的余弦值.
解:法一 :以A点为原点,AB为x轴,AD为y轴,AD为z轴的空间直角坐标系,
则依题意可知相关各点的坐标分别是A(0,0,0),B(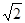 ,0,0),C(
,0,0),C(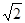 ,1,0),
,1,0),
D(0,1,0),S(0,0,1)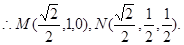 ……………………2分
……………………2分
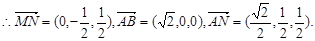 …………………………4分
…………………………4分
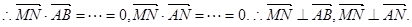
∴MN⊥平面ABN.………………………………………6分
(2)设平面NBC的法向量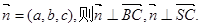 且又易知
且又易知
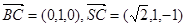
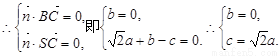
令a=1,则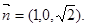 ……………………………………9分
……………………………………9分
显然,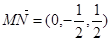 就是平面ABN的法向量.
就是平面ABN的法向量.
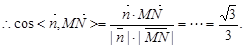 ………………………………………10分
………………………………………10分
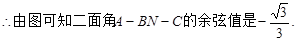 ………………………………………12分
………………………………………12分
法二:(1)由题意知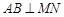 连
连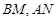 则可求
则可求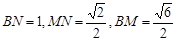 ,则
,则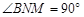
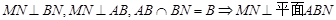 …………………………6分
…………………………6分
(2)因为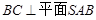 ,在平面
,在平面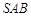 内作
内作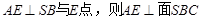 且
且 ,
,
又在 ,所以
,所以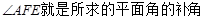 ,
,
且 故所求的二面角的余弦值为
故所求的二面角的余弦值为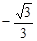 ………………………12分
………………………12分
考点:本题主要考查向量法证明直线与平面的垂直,二面角的求法,考查学生计算能力,逻辑思维能力,是中档题.
点评:解决该试题的关键是合理的建立空间直角坐标系,然后准确的表示点的坐标,和法向量的坐标,进而得到垂直的判定和二面角的平面角的求解。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
