题目内容
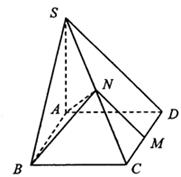
((10分).如图所示,已知四棱锥P—ABCD,底面ABCD为菱形,PA⊥平面ABCD,
∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:AE⊥PD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为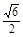 ,
,
求二面角E—AF—C的余弦值.
【答案】

【解析】
(1)证明 由四边形ABCD为菱形,∠ABC=60°,
可得△ABC为正三角形.因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而PA 平面PAD,AD
平面PAD,AD 平面PAD且PA∩AD=A,
平面PAD且PA∩AD=A,
所以AE⊥平面PAD.又PD 平面PAD,所以AE⊥PD.
平面PAD,所以AE⊥PD.
(2)解 如图所示,设AB=2,H为PD上任意一点,连结AH、EH,
 由(1)知,AE⊥平面PAD,
由(1)知,AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE= ,
,
所以,当AH最短时,∠EHA最大,即当AH⊥PD时,∠EHA最大.
此时,tan∠EHA= =
= =
= ,因此AH=
,因此AH= .又AD=2,所以∠ADH=45°,所以PA=2.
.又AD=2,所以∠ADH=45°,所以PA=2.
方法一 因为PA⊥平面ABCD,PA 平面PAC,
平面PAC,
所以,平面PAC⊥平面ABCD.过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E—AF—C的平面角.
在Rt△AOE中,EO=AE·sin30°= ,AO=AE·cos30°=
,AO=AE·cos30°= ,又F是PC的中点,
,又F是PC的中点,
在Rt△ASO中,SO=AO·sin45°= ,
,
又SE= =
= =
= ,
,
在Rt△ESO中,cos∠ESO= =
= =
= ,
,
即所求二面角的余弦值为 .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
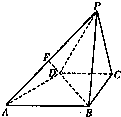 如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足
如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且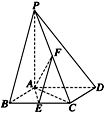

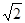 .
.