题目内容
1+log2x=2log2(x-a)恰有一个实数解,则a的取值范围为 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:首先化简1+log2x=2log2(x-a),可得log22x=2log2(x-a),所以
;然后根据关于x的二元一次方程恰有一个实数解,可得直线y=x-a与曲线y=
在平面直角坐标系中有且只有一个交点,分别画出直线y=x-a与曲线y=
的图象,判断出a的取值范围即可.
|
| 2x |
| 2x |
解答:
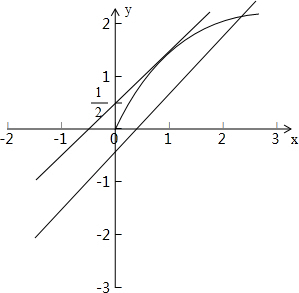 解:由1+log2x=2log2(x-a),
解:由1+log2x=2log2(x-a),
可得log22x=2log2(x-a),
所以
;
因为关于x的二元一次方程恰有一个实数解,
所以直线y=x-a与曲线y=
在平面直角坐标系中有且只有一个交点,
①当直线y=x-a与曲线y=
相切时,
由x-a=
,可得x2-2(a+1)x+a2=0,
△=0,可得4(a+1)2-4a2=0,
解得a=-
;
②根据图象,可得当-a≤0,即a≥0时,直线y=x-a与曲线y=
恒有一个交点,
综上,a的取值范围为:a≥0或a=-
.
故答案为:a≥0或a=-
.
 解:由1+log2x=2log2(x-a),
解:由1+log2x=2log2(x-a),可得log22x=2log2(x-a),
所以
|
因为关于x的二元一次方程恰有一个实数解,
所以直线y=x-a与曲线y=
| 2x |
①当直线y=x-a与曲线y=
| 2x |
由x-a=
| 2x |
△=0,可得4(a+1)2-4a2=0,
解得a=-
| 1 |
| 2 |
②根据图象,可得当-a≤0,即a≥0时,直线y=x-a与曲线y=
| 2x |
综上,a的取值范围为:a≥0或a=-
| 1 |
| 2 |
故答案为:a≥0或a=-
| 1 |
| 2 |
点评:本题主要考查了根的存在性以及根的个数的判断,考查了数形结合的运用,属于中档题,解答此题的关键是分析出直线y=x-a与曲线y=
在平面直角坐标系中有且只有一个交点,并分别画出它们的图象.
| 2x |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若
如图,在扇形OAB中,∠AOB=60°,C为弧AB上的一个动点.若