题目内容
如图，已知椭圆| x2 |
| 4 |
考点：椭圆的简单性质
专题：证明题,圆锥曲线的定义、性质与方程
分析：由已知条件，利用直线方程的截距式分别求出点P，Q的横坐标的表达式，再利用椭圆的方程即可证明结论．
解答：
证明：设M（x0，y0），P（p，0），Q（q，0）．
由直线方程的截距式及M，P，B1三点共线，得到
-
=1，∴p=
，
由直线方程的截距式及M，P，B2三点共线，得到
+
=1，q=
，
∴|OP|•|OQ|=|pq|=
=4．
由直线方程的截距式及M，P，B1三点共线，得到
| x0 |
| p |
| y0 |
| b |
| x0 |
| 1+y0 |
由直线方程的截距式及M，P，B2三点共线，得到
| x0 |
| q |
| y0 |
| b |
| x0 |
| 1-y0 |
∴|OP|•|OQ|=|pq|=
| x02 |
| 1-y02 |
点评：本题考查椭圆的应用，涉及到直线的截距式方程、椭圆等知识点，综合性强，解题时要注意等价转化思想的合理运用．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
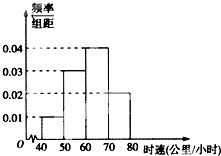已知某一段公路限速60公里/小时，现抽取200辆通过这一段公路的汽车的时速，其频率分布直方图如图所示，则这200辆汽车中在该路段没有超速的有