题目内容
10.已知集合A={x|x≥2},B={x||x-m|≤1},若A∩B=B,则实数m的取值范围是[3,+∞).分析 先求出集合B,再利用交集定义和不等式性质求解.
解答 解:∵集合A={x|x≥2},B={x||x-m|≤1}={x|m-1≤x≤m+1},
A∩B=B,
∴m-1≥2,解得m≥3,
∴实数m的取值范围是[3,+∞).
故答案为:[3,+∞).
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意不等式性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知a∈R,不等式$\frac{x-3}{x+a}>1$的解集为P,且-4∉P,则a的取值范围是( )
| A. | a≥-4 | B. | -3<a≤4 | C. | a≥4或a≤-3 | D. | a≥4或a<-3 |
20.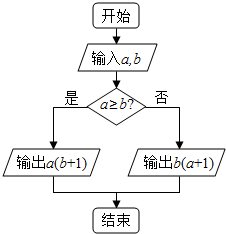 对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
 对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )
对于实数a和b,定义运算a*b,运算原理如图所示,则式子($\frac{1}{2}$)-2*lne3的值为( )| A. | 8 | B. | 15 | C. | 16 | D. | $\frac{3}{2}$ |
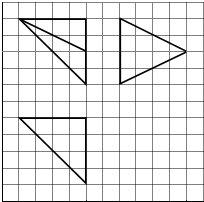 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )