Question

已知函数y=cos（2x+

π

3

）．
（1）用“五点法”作出它在长度为一个周期的闭区间上的简图；（自己做出坐标系，并标出横纵坐标）
（2）求使函数y取最大值和最小值时自变量x的集合，并求出它的最大值和最小值；
（3）指出该函数的增区间和减区间．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）根据五点法作图的步骤，作出函数y=Asin（ωx+φ）在一个周期上的简图．
（2）根据余弦函数的图象特征，数形结合求出函数y取最大值和最小值时自变量x的集合，并求出它的最大值和最小值．
（3）结合所作的函数的图象、函数的周期性，指出该函数的增区间和减区间．

解答： 解：（1）列表：

2x+ π 3	0	π 2	π	3π 2	2π
x	- π 6	π 12	π 3	7π 12	5π 6
y	1	0	-1	0	1

描点作图：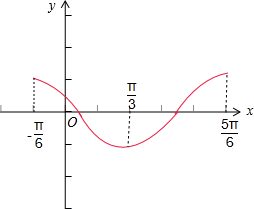
（2）当2x+

π

3

=2kπ，k∈z，即 当x=kπ-

π

6

时，函数取得最大值为1；当2x+

π

3

=2kπ+π，k∈z，即 当x=kπ+

π

3

、k∈z时，函数取得最小值为-1．
（3）由函数的图象可得，函数的增区间为[kπ+

π

3

，kπ+

5π

6

]，k∈z；减区间为[kπ-

π

6

，kπ+

π

3

]，k∈z．

点评：本题主要考查用五点法作函数y=Asin（ωx+φ）在一个周期上的简图，余弦函数的单调性和最值，属于基础题．