题目内容
在数列{an}中,前n项和Sn满足2Sn=(n+2)an-1.
(1)求数列{an}的通项公式;
(2)求Tn=
+
+…+
的值.
(1)求数列{an}的通项公式;
(2)求Tn=
| 1 |
| a1a3 |
| 1 |
| a2a4 |
| 1 |
| anan+2 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由2Sn=(n+2)an-1求出首项,取n=n-1得另一递推式,作差后可得
=
(n≥2),然后利用累积法求数列的通项公式;
(2)把数列{an}的通项公式代入
,整理后利用裂项相消法求Tn=
+
+…+
的值.
| an |
| an-1 |
| n+1 |
| n |
(2)把数列{an}的通项公式代入
| 1 |
| anan+2 |
| 1 |
| a1a3 |
| 1 |
| a2a4 |
| 1 |
| anan+2 |
解答:
解:(1)由2Sn=(n+2)an-1,得2S1=2a1=(1+2)a1-1,即a1=1;
当n≥2时,有2Sn-1=(n-1+2)an-1-1,
∴2an=(n+2)an-(n+1)an-1,即
=
(n≥2),
∴an=
•
…
•a1=
•
…
•1=
(n≥2).
n=1时上式成立,
∴an=
;
(2)
=
=
=2(
-
),
∴Tn=
+
+…+
=2[(
-
)+(
-
)+(
-
)+…+(
-
)]
=2(
+
-
-
)=
.
当n≥2时,有2Sn-1=(n-1+2)an-1-1,
∴2an=(n+2)an-(n+1)an-1,即
| an |
| an-1 |
| n+1 |
| n |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
| n+1 |
| n |
| n |
| n-1 |
| 3 |
| 2 |
| n+1 |
| 2 |
n=1时上式成立,
∴an=
| n+1 |
| 2 |
(2)
| 1 |
| anan+2 |
| 1 | ||||
|
| 4 |
| (n+1)(n+3) |
| 1 |
| n+1 |
| 1 |
| n+3 |
∴Tn=
| 1 |
| a1a3 |
| 1 |
| a2a4 |
| 1 |
| anan+2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| n+3 |
=2(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 5n2+15n+5 |
| 3(n+2)(n+3) |
点评:本题考查了数列递推式,考查了利用累积法求数列的通项公式,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知直线m、n和平面α,则m∥n的必要非充分条件是( )
| A、m、n与α成等角 |
| B、m⊥α且n⊥α |
| C、m∥α且n?α |
| D、m∥α且n∥α |
某班级有6名同学去报名参加校学生会的4项社团活动,若甲、乙两位同学不参加同一社团,每个社团都有人参加,每人只参加一个社团,则不同的报名方案数为( )
| A、4320 | B、2400 |
| C、2160 | D、1320 |
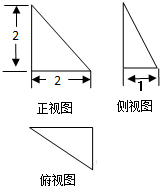 已知某几何体的三视图如图所示,三个视图都为直角三角形,其中主视图是以2为直角边的等腰直角三角形,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,三个视图都为直角三角形,其中主视图是以2为直角边的等腰直角三角形,则该几何体的外接球的表面积为( )| A、16π | B、9π | C、8π | D、4π |
已知函数f(x)=
若数列{an}满足an=f(n)(n∈N+),且{an}是递增数列,则实数a的取值范围是( )
|
A、[
| ||
B、(
| ||
| C、(2,3) | ||
| D、(1,3) |
设F为双曲线
-
=1(a>0,b>0)的右焦点,若双曲线与渐近线在第一象限分别存在点PQ.使得P为QF的中点,则双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(2,+∞ | ||
C、(1,
| ||
D、(
|