Question

14．已知f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{1-x，0＜x＜1}\\{\sqrt{x-1}，x≥1}\end{array}\right.$，若a＜b＜c，f（a）=f（b）=f（c），则实数a+3b+c的取值范围是（-∞，$\frac{11}{4}-ln2$]．

Answer 1

分析 通过分段函数求出a，b，c，得到a+3b+c的表达式，通过构造函数利用函数的导数求解函数的最值，推出结果即可．

解答 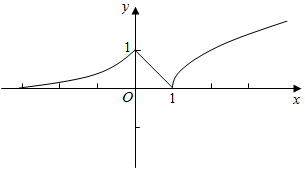解：f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{1-x，0＜x＜1}\\{\sqrt{x-1}，x≥1}\end{array}\right.$，若a＜b＜c，f（a）=f（b）=f（c），
令f（a）=f（b）=f（c）=t，
可得a=lnt，b=1-t，c=t²+1，t∈（0，1）．
则：a+3b+c=lnt+t²-3t+4，t∈（0，1）．
令f（t）=lnt+t²-3t+4，t∈（0，1）．
则f′（t）=$\frac{1}{t}$+2t-3=$\frac{（2t-1）（t-1）}{t}$，t∈（0，1）．
当$\frac{（2t-1）（t-1）}{t}$=0解得t=1或t=$\frac{1}{2}$，
t∈（0，$\frac{1}{2}$）时，f′（t）＞0，f（t）是增函数．t∈（$\frac{1}{2}$，1）时，f′（t）＜0，f（t）是减函数．
t=$\frac{1}{2}$时，函数取得最大值：$\frac{11}{4}-ln2$．
t→0时，函数f（t）趋向于-∞，无最小值．
实数a+3b+c的取值范围是：（-∞，$\frac{11}{4}-ln2$]．
故答案为：（-∞，$\frac{11}{4}-ln2$]．

点评 本题考查函数的导数的综合应用，数形结合，考查分析问题解决问题的能力，转化思想的应用．