题目内容
9.已知O是锐角三角形ABC的外接圆圆心,tanA=$\frac{1}{2}$,$\frac{cosB}{sinC}$$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$=2m$\overrightarrow{AO}$,则m=$\frac{{2\sqrt{5}}}{5}$.分析 取AB的中点D,则$\overrightarrow{AO}$=$\overrightarrow{AD}$+$\overrightarrow{DO}$,从而可得$\frac{cosB}{sinC}$$\overrightarrow{AB}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$•$\overrightarrow{AB}$=2m($\overrightarrow{AD}$+$\overrightarrow{DO}$)•$\overrightarrow{AB}$,从而可得m=$\frac{cosB+cosAcosC}{sinC}$=sinA,从而解得.
解答  解:取AB的中点D,则$\overrightarrow{AO}$=$\overrightarrow{AD}$+$\overrightarrow{DO}$,
解:取AB的中点D,则$\overrightarrow{AO}$=$\overrightarrow{AD}$+$\overrightarrow{DO}$,
代入$\frac{cosB}{sinC}$$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$=2m$\overrightarrow{AO}$得,
$\frac{cosB}{sinC}$$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$=2m($\overrightarrow{AD}$+$\overrightarrow{DO}$),
∵$\overrightarrow{OD}$⊥$\overrightarrow{AB}$,∴$\overrightarrow{OD}$•$\overrightarrow{AB}$=0;
∴$\frac{cosB}{sinC}$$\overrightarrow{AB}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$$\overrightarrow{AC}$•$\overrightarrow{AB}$=2m($\overrightarrow{AD}$+$\overrightarrow{DO}$)•$\overrightarrow{AB}$,
∴$\frac{cosB}{sinC}$c2+$\frac{cosC}{sinB}$bcosA=mc2,
由$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$化简可得,
$\frac{cosB}{sinC}$sin2C+$\frac{cosC}{sinB}$sinBsinCcosA=msin2C,
∴m=$\frac{cosB+cosAcosC}{sinC}$=sinA,
又∵tanA=$\frac{1}{2}$,
∴sinA=$\frac{\frac{1}{2}}{\sqrt{1+\frac{1}{4}}}$=$\frac{{2\sqrt{5}}}{5}$,
故答案为:$\frac{{2\sqrt{5}}}{5}$.
点评 本题考查了平面向量的运算及解三角形的运算应用,同时考查了数形结合的思想方法应用,属于中档题.

 53随堂测系列答案
53随堂测系列答案附表(临界值表):
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 只有不超过1%的把握认为“爱好该项运动与性别有关” | |
| C. | 有99%以上的把握认为“爱好该项运动与性别有关” | |
| D. | 有99%以上的把握认为“爱好该项运动与性别无关” |
| A. | 0 | B. | 1 | C. | 2 | D. | 不能确定 |
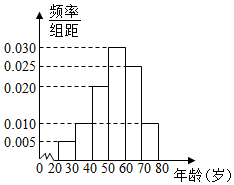 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80],得到如图的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80],得到如图的频率分布直方图.