题目内容
已知圆(x-a)2+(y-b)2=1与二直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,则
的取值范围为( )
| b |
| a-2 |
A、[-
| ||||
B、[
| ||||
C、(-∞,-
| ||||
D、[-
|
考点:直线与圆的位置关系
专题:直线与圆
分析:圆(x-a)2+(y-b)2=1与二直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,可得圆心C到直线的距离小于等于半径,即可求
的取值范围.
| b |
| a-2 |
解答:
解:∵圆:(x-a)2+(y-b)2=1,圆心为C(a,b),半径为1.
∵直线l1:3x-4y-1=0和圆:(x-a)2+(y-b)2=1有公共点,
∴圆心C到直线的距离:
≤1,即
…①
∵直线l2:4x+3y+1=0和圆:(x-a)2+(y-b)2=1有公共点,
∴圆心C到直线的距离:
≤1,即
…②
∴作出①②不等式组表示的平面区域如图:
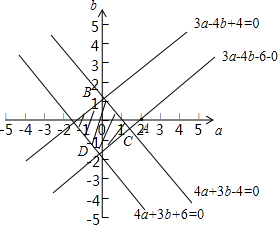
∴由
得B(
,
).A(2,0).
∴由
的几何意义可得,最大值为kAC=
,最小值为kAB=
=-
,
∴
的取值范围为[-
,
].
故选:D.
∵直线l1:3x-4y-1=0和圆:(x-a)2+(y-b)2=1有公共点,
∴圆心C到直线的距离:
| |3a-4b-1| |
| 5 |
|
∵直线l2:4x+3y+1=0和圆:(x-a)2+(y-b)2=1有公共点,
∴圆心C到直线的距离:
| |4a+3b+1| |
| 5 |
|
∴作出①②不等式组表示的平面区域如图:

∴由
|
| 4 |
| 25 |
| 28 |
| 25 |
∴由
| b |
| a-2 |
| 3 |
| 4 |
| ||
|
| 14 |
| 23 |
∴
| b |
| a-2 |
| 14 |
| 23 |
| 3 |
| 4 |
故选:D.
点评:本题考查直线与圆的位置关系,考查点到直线距离公式的运用,考查学生的计算能力,

练习册系列答案
相关题目
若α,β,γ表示平面,m,n表示直线,则下列命题中,正确的是( )
| A、m?α,n?α,m∥β,n∥β,则α∥β |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若α∥β,m?α,n?β,则m∥n |
| D、若α∥β,m?α,则m∥β |
下列判断,正确的是( )
| A、平行于同一平面的两直线平行 |
| B、垂直于同一直线的两直线平行 |
| C、垂直于同一平面的两平面平行 |
| D、垂直于同一平面的两直线平行 |
过点P(-1,4)作圆x2+y2-4x-6y+12=0的切线,则切线长为( )
| A、3 | ||
B、
| ||
C、
| ||
| D、5 |