题目内容
已知圆C1是经过点A(0,2)和B(2,-2)的所有圆中周长最小的圆,
(1)求圆C1的方程;
(2)若圆C1与圆C2:x2+y2-6x-2y+5=0相交于点C、D,求公共弦长|CD|.
(1)求圆C1的方程;
(2)若圆C1与圆C2:x2+y2-6x-2y+5=0相交于点C、D,求公共弦长|CD|.
考点:圆的标准方程
专题:直线与圆
分析:(1)当AB为圆C1的直径时,周长最小,求得圆心C1的坐标和半径的值,可得圆C1的方程.
(2)把圆C1的方程和圆C2的方程相减,可得公共弦方程,求得圆C1到公共弦的距离d,再由弦长公式求得弦长|AB|的值.
(2)把圆C1的方程和圆C2的方程相减,可得公共弦方程,求得圆C1到公共弦的距离d,再由弦长公式求得弦长|AB|的值.
解答:
解:(1)当AB为圆C1的直径时,周长最小,则圆心C1(1,0),
半径r=
=
,∴圆C1的方程为:(x-1)2+y2=5.
(2)把圆C1的方程和圆C2的方程相减,可得公共弦方程为:4x+2y-9=0,
∴圆C1到公共弦的距离为d=
=
,
则由弦长公式可得
=
=
,所以|AB|=
.
半径r=
| (1-0)2+(0-2)2 |
| 5 |
(2)把圆C1的方程和圆C2的方程相减,可得公共弦方程为:4x+2y-9=0,
∴圆C1到公共弦的距离为d=
| |4-9| | ||
|
| ||
| 2 |
则由弦长公式可得
| |AB| |
| 2 |
(
|
| ||
| 2 |
| 15 |
点评:本题主要考查求圆的标准方程,直线和圆相交的性质,点到直线的距离公式、弦长公式的应用,属于基础题.

练习册系列答案
相关题目
已知圆(x-a)2+(y-b)2=1与二直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,则
的取值范围为( )
| b |
| a-2 |
A、[-
| ||||
B、[
| ||||
C、(-∞,-
| ||||
D、[-
|
已知直线m,n和平面α,满足m?α,n∥α,则直线m,n的关系是( )
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
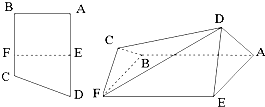 如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.
如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.