题目内容
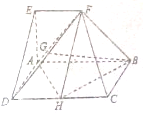 如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD
如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD(Ⅰ)若G为DF的中点,求BG的长,
(Ⅱ)若H是DC的中点,求二面角A-HF-B的余弦值.
考点:平面与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离
分析:(Ⅰ)由已知可求BF,ED,DF,DB,FG,DF的值,可知DB2=BF2+DF2,由勾股定理可知DF⊥BF,从而可求BG的值.
(Ⅱ)由已知可求得△AHF,△BFH都是正三角形,取FH的中点M,连接AM,BM,可得AM⊥FH,BM⊥FH,∠AMB即为二面角A-HF-B,分别求出AB,AM,BM的值,从而由余弦定理可求二面角A-HF-B的余弦值.
(Ⅱ)由已知可求得△AHF,△BFH都是正三角形,取FH的中点M,连接AM,BM,可得AM⊥FH,BM⊥FH,∠AMB即为二面角A-HF-B,分别求出AB,AM,BM的值,从而由余弦定理可求二面角A-HF-B的余弦值.
解答:
解:(Ⅰ)∵四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD,G为DF的中点,
∴BF=
,ED=
,DF=
=
,DB=
=
,FG=
,DF=
∴DB2=BF2+DF2
∴由勾股定理可知DF⊥BF
∴BG=
=
=

(Ⅱ)∵四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD,G为DF的中点,
∴BF=
,BH=
,AH=
,AF=
,FH=
∴△AHF,△BFH都是正三角形
∴取FH的中点M,连接AM,BM,可得AM⊥FH,BM⊥FH,∠AMB即为二面角A-HF-B,
∵AB=2,AM=
=
=
=BM
∴由余弦定理知,cos∠AMB=
=
=-
.
故二面角A-HF-B的余弦值是-
.
∴BF=
| 2 |
| 2 |
| EF2+ED2 |
| 3 |
| AD2+AB2 |
| 5 |
| 1 |
| 2 |
| ||
| 2 |
∴DB2=BF2+DF2
∴由勾股定理可知DF⊥BF
∴BG=
| BF2+FG2 |
2+
|
| ||
| 2 |

(Ⅱ)∵四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD,G为DF的中点,
∴BF=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴△AHF,△BFH都是正三角形
∴取FH的中点M,连接AM,BM,可得AM⊥FH,BM⊥FH,∠AMB即为二面角A-HF-B,
∵AB=2,AM=
| AH2-HM2 |
2-
|
| ||
| 2 |
∴由余弦定理知,cos∠AMB=
| AM2+BM2-AB2 |
| 2×AM×BM |
| ||||||||
2×
|
| 1 |
| 3 |
故二面角A-HF-B的余弦值是-
| 1 |
| 3 |
点评:本题主要考查了平面与平面垂直的判定,二面角的平面角及求法,其中正确作出二面角是解题的关键,属于中档题.

练习册系列答案
相关题目
已知集合A={(x,y)|
},点P(x1,y1),Q(x2,y2)且(x1,y1)∈A,(x2,y2)∈A,
=(1,-1),则
•
的最大值为( )
|
| a |
| a |
| PQ |
| A、5 | ||
| B、4 | ||
| C、3 | ||
D、
|
已知抛物线y=
x2与双曲线
-x2=1(a>0)有共同的焦点F,O为坐标原点,P在x轴上方且在双曲线上,则
•
的最小值为( )
| 1 |
| 8 |
| y2 |
| a2 |
| OP |
| FP |
A、2
| ||
B、3-2
| ||
C、
| ||
D、
|
 只是2问,用空间向量啊!以c为坐标原点哦!
只是2问,用空间向量啊!以c为坐标原点哦!