题目内容
已知集合A={(x,y)|
},点P(x1,y1),Q(x2,y2)且(x1,y1)∈A,(x2,y2)∈A,
=(1,-1),则
•
的最大值为( )
|
| a |
| a |
| PQ |
| A、5 | ||
| B、4 | ||
| C、3 | ||
D、
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,直线与圆
分析:作出集合A表示的平面区域,运用向量的数量积的坐标表示,再由P,Q的位置,即可得到最大值.
解答:
 解:作出集合A表示的平面区域,
解:作出集合A表示的平面区域,
则
•
=(1,-1)•(x2-x1,y2-y1)
=x2-x1+y1-y2,
要求最大值,则Q与A重合,即为(2,0),
P与B重合,由2x+y=4和4x-y=-1解得,交点为(0.5,3),
则有所求最大值为2-0.5+3-0=4.5,
故选D.
 解:作出集合A表示的平面区域,
解:作出集合A表示的平面区域,则
| a |
| PQ |
=x2-x1+y1-y2,
要求最大值,则Q与A重合,即为(2,0),
P与B重合,由2x+y=4和4x-y=-1解得,交点为(0.5,3),
则有所求最大值为2-0.5+3-0=4.5,
故选D.
点评:本题考查平面向量的数量积的坐标表示,考查不等式表示的平面区域,考查最值的求法,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
一个几何体的三视图如图所示,其中俯视图为正三角形,则该几何体的外接球体积为( )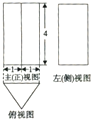

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,若f(t)+f(t+2)>0,则实数t的取值范围是( )
|
A、t<-3-
| ||||
| B、t>-1 | ||||
C、t<1-
| ||||
| D、t<-2 |
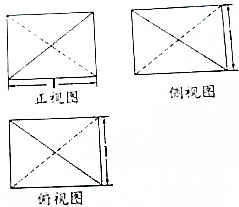
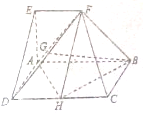 如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD
如图,在五面体ABCDEF中,四边形ABCD是矩形,AB∥EF,AB=2EF=2,AE=AD=1,∠EAB=90°,平面ABFE⊥平面ABCD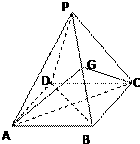 如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2,G是PB的中点.
如图,四棱锥中,底面是边长为2的正方形,顶点在底面的射影是底面的中心,侧棱长为2,G是PB的中点.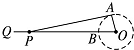 如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于
如图为曲柄连杆结构示意图,当曲柄 OA 在 OB 位置时,连杆端点 P 在 Q 的位置,当 OA 自 OB 按顺时针旋转 α 角时,P 和 Q 之间的距离为 x,已知 OA=25cm,AP=125cm,若 OA⊥AP,则 x 等于