题目内容

14．已知圆x2+y2-2x+my-4=0上两点M，N关于直线2x+y=0对称，则圆的方程为（　　）
A．（x-1）2+（y+2）2=3B．（x-1）2+（y+2）2=9C．（x-1）2+（y-2）2=4D．（x-1）2+（y-2）2=12

分析 求出圆的圆心，代入直线方程即可求出m的值，然后求出圆的半径，即可求出圆的方程．

解答 解：因为圆x2+y2-2x+my-4=0上两点M、N关于直线2x+y=0对称，
所以直线经过圆的圆心，
圆x2+y2-2x+my-4=0的圆心坐标（1，-$\frac{m}{2}$），
所以2×1-$\frac{m}{2}$=0，m=4．
所以圆的半径为：$\frac{1}{2}\sqrt{（-2）^{2}+{4}^{2}+4×4}$=3，
所以圆的方程为（x-1）2+（y+2）2=9
故选B

点评 本题考查直线与圆的位置关系，求出圆的圆心坐标代入直线方程，是解题的关键．

练习册系列答案
相关题目
4．已知等差数列{an}的首项a1=1，公差d≠0，且a2是a1与a4的等比中项，则d=（　　）
A．1B．2C．3D．4
5．向量$\overrightarrow a$=（sinx，cosx），$\overrightarrow b$=（sinx，sinx），$\overrightarrow c$=（-1，0）．
（Ⅰ）若x=$\frac{π}{3}$，求向量$\overrightarrow a$、$\overrightarrow c$的夹角；
（Ⅱ）若x∈$[-\frac{3π}{8}，\frac{π}{4}]$，函数$f（x）=λ\overrightarrow a•\overrightarrow b$的最大值为$\frac{1}{2}$，求λ的值．
2．已知数列{an}中的相邻两项a2k-1，a2k是关于x的方程x2-（3k+2k）x+3k•2k=0的两个根，且a2k-1≤a2k（k=1，2，3，…）
（1）求a1，a3，a5，a7；
（2）求数列{an}的前2n项和S2n；
（3）记$f（n）=\frac{1}{2}（\frac{|sinn|}{sinn}+3）$，${T_n}=\frac{{{{（-1）}^{f（2）}}}}{{{a_1}{a_2}}}+\frac{{{{（-1）}^{f（3）}}}}{{{a_3}{a_4}}}+\frac{{{{（-1）}^{f（4）}}}}{{{a_5}{a_6}}}+…+\frac{{{{（-1）}^{f（n+1）}}}}{{{a_{2n-1}}{a_{2n}}}}$，求Tn的最值．
9．若x＞y，m＞n，下列不等式正确的是（　　）
A．x-m＞y-nB．xm＞ynC．nx＞myD．m-y＞n-x
19．在下面给出的条件中，若条件足够能推出a∥α，则在横线上填“OK”；若条件不能保证推出a∥α，则请在横线上补足条件：
（1）条件：a∥b，b∥c，c?α，a?α，结论：a∥α，
（2）条件：α∩β=b，a∥b，a?β，OK，结论：a∥α．
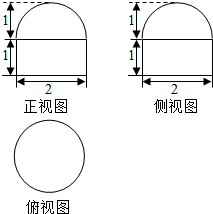6．已知一个空间组合体的三视图如图所示，其中正视图、侧视图都是由半圆和矩形组成，请说出该组合体由哪些几何体组成，并且求出该组合体的表面积和体积．
3．函数$f（x）=\sqrt{\frac{1}{4}-{2^x}}$的定义域是（-∞，-2]．
4．记集合A={（x，y）|x2+y2≤16}和集合B={（x，y）|x+y-4≤0，x≥0，y≥0}表示的平面区域分别为Ω1，Ω2，若在区域Ω1内任取一点M（x，y），则点M落在区域Ω2的概率为$\frac{1}{2π}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网