题目内容
7．若向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），则2$\overrightarrow{a}$-$\overrightarrow{b}$的坐标为（ ）| A． | （1，5） | B． | （1，1） | C． | （5，4） | D． | （3，5） |
分析 由向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），利用向量的坐标运算法则能求出2$\overrightarrow{a}$-$\overrightarrow{b}$的坐标．
解答 解：∵向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），
∴2$\overrightarrow{a}$-$\overrightarrow{b}$=（4，6）-（-1，2）=（5，4）．
故选：C．
点评 本题考查平面向量坐标求法，是基础题，解题时要认真审题，注意向量的坐标运算法则的合理运用．
练习册系列答案
相关题目
17．函数f（x）=$\frac{1}{2-x}$+$\sqrt{9-{x}^{2}}$的定义域为（ ）
| A． | {x|x≠2} | B． | {x|x＜-3或x＞3} | C． | {x|-3≤x≤3} | D． | {x|-3≤x≤3且≠2} |
18．函数 y=sin$\frac{x}{2}$，x∈R的最小正周期是（ ）
| A． | 4π | B． | 2π | C． | π | D． | $\frac{π}{2}$ |
15．
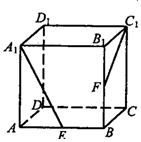如图，ABCD-A1B1C1D1是正方体，E、F分别是AB、BB1的中点，则异面直线A1E与C1F所成角的余弦值为（ ）
如图，ABCD-A1B1C1D1是正方体，E、F分别是AB、BB1的中点，则异面直线A1E与C1F所成角的余弦值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{5}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
2．若抛物线y2=2px，准线方程为x=-2，则p的值为（ ）
| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
12．若a=0.32，b=log20.3，c=20.3，则a，b，c三个数的大小关系是（ ）
| A． | c＜a＜b | B． | b＜c＜a | C． | c＜b＜a | D． | b＜a＜c |
18．设集合A={x|x2＜4}，B={1，2，3}，则A∩B=（ ）
| A． | {1，2，3} | B． | {1，2} | C． | {1} | D． | {2} |
19．已知全集U={x∈N|y=lg（5-x）}，M={x∈Z|1≤2x≤4），N={2，3}，则（∁UM）∩N=（ ）
| A． | {2} | B． | {3} | C． | {2，3，4} | D． | {0，1，2，3，4} |