题目内容
3.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率等于( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点在x轴上,a=5,b=4,c=$\sqrt{{a}^{2}-{b}^{2}}$=3,椭圆的离心率e=$\frac{c}{a}$=$\frac{3}{5}$,即可求得答案.
解答 解:由题意可知:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点在x轴上,a=5,b=4,c=$\sqrt{{a}^{2}-{b}^{2}}$=3,
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{3}{5}$,
椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率$\frac{3}{5}$,
故选B.
点评 本题考查椭圆的标准方程及简单几何性质,考查椭圆的离心率公式的应用,属于基础题.

练习册系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{-(x+1)^{2}+1,x<0}\\{{2}^{x}-1,x≥0}\end{array}\right.$,若函数g(x)=f(x)-a有三个零点,则实数a的取值范围是( )
| A. | (0,1) | B. | [0,1) | C. | (0,1] | D. | [0,1] |
14.已知集合M={1,2,3},N={1,3,4},则M∩N=( )
| A. | {1,3} | B. | {1,2,3,4} | C. | {2,4} | D. | {1,3,4} |
11.已知α,β,γ是空间三个不重合的平面,m,n是空间两条不重合的直线,则下列命题为真命题的是( )
| A. | 若α⊥β,β⊥γ,则α∥γ | B. | 若α⊥β,m∥β,则m⊥α | C. | 若m⊥α,n⊥α,则m∥n | D. | 若m∥α,n∥α,则m∥n |
18.函数 y=sin$\frac{x}{2}$,x∈R的最小正周期是( )
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
8.已知x>0,则x+$\frac{4}{x}$-1的最小值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.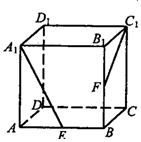 如图,ABCD-A1B1C1D1是正方体,E、F分别是AB、BB1的中点,则异面直线A1E与C1F所成角的余弦值为( )
如图,ABCD-A1B1C1D1是正方体,E、F分别是AB、BB1的中点,则异面直线A1E与C1F所成角的余弦值为( )
 如图,ABCD-A1B1C1D1是正方体,E、F分别是AB、BB1的中点,则异面直线A1E与C1F所成角的余弦值为( )
如图,ABCD-A1B1C1D1是正方体,E、F分别是AB、BB1的中点,则异面直线A1E与C1F所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
12.若a=0.32,b=log20.3,c=20.3,则a,b,c三个数的大小关系是( )
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |